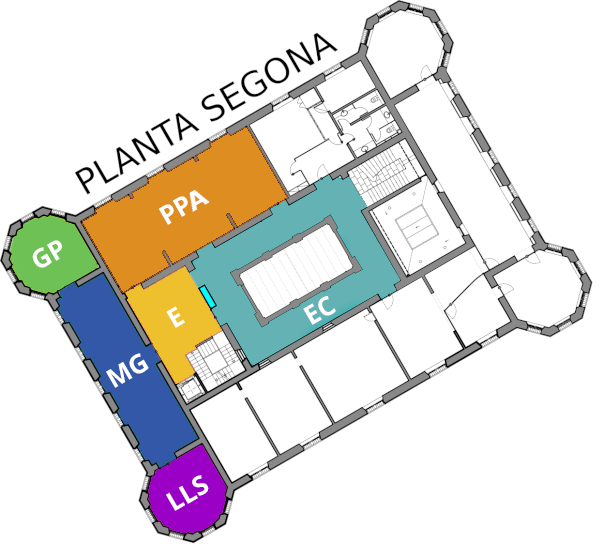
second floor

Martin Gardner Room
Combinatorics, tiling and Leonardo bridge.
In this room you will find modules of combinatorics, graphs, strategy, tiling and the Leonardo bridge.

Who was Martin Gardner?
Martin Gardner (Oklahoma, 1914 – 2010) was one of the most renowned mathematics communicators of the 20th century.
For many generations, his books and articles have been the gateway to a fascination with mathematics from play, magic, art, chess, cryptography or literature.
Despite being a man of letters, having a degree in philosophy and a journalist, he was awarded by the American Mathematical Society for his work presenting mathematical issues in an interesting and clear way while collaborating with renowned mathematicians.
In October of each year, in coordination with enthusiasts from all over the world, the MMACA celebrates Martin Gardner's feast in remembrance of his birth.

Some modules in this room
It is necessary to move the tower by moving the discs one by one and always leaving the little ones on the grains.
Put the pieces so that the colors are not on the side. It is a version of the 4 color theorem.
Place the 16 pieces without either repeating colors or numbers in rows or columns.
Col·loca les peces d’aquesta divisió del pla tenint en compte que estan formades pels punts més propers a cada clavilla.
Set hexàgons on s’han de fer coincidir els colors
Col·loca les fitxes de manera que els colors dels costats que es toquen coincideixin.
Col·loca les cares dels cubs i del dodecaedre de forma que coincideixin els colors
Make as many different sets as possible got-spoon-knife.
The puzzle of rebuilding the chessboard that seems difficult, but that the organization facilitates.
Put the skyscrapers taking into account how many you see from each position.
Reconstrueix el cub de 3x3x3
Una rajola que pot enrajolar el pla però només de forma no periòdica.
Un circuit amb 3 cotxes i diferents reptes per situar-los tenint en compte l’ordre i la orientació
Dues rajoles que omplen l’espai de forma no periòdica
With the chain we take a tour that passes through all the vertices of the dodecaedre
Build this bridge, without any support, devised by Leonardo
How do more cylinders fit?
In gridded mesh or in triangular mesh.
Put the fences of the pens, the figures indicate the amount of fences around them.
Un bitllet de 50€ reconstruït com un de 100€ ?
Reconstruir un quadrat amb quadrats.
En qualsevol grup de sis persones, sempre: o hi ha 3 que es coneixen mútuament o bé 3 que no es coneixen.





















