Pone las 4 baldosas entre los dos espejos y mira el mosaico infinito que has creado.

- Ubicación: Sala Emma Castelnouvo
- Edad mínima: a partir de 6 años.
- Tiempo requerido: 5 minutos.
- Número de participantes: Una o más personas
- Palabras clave: baldosa de cartabón, baldosa de pañuelo, reflexión, simetría, friso, mosaico
- Taxonomía: Geometría, arte
Las baldosas de cartabón o baldosas de pañuelo
Esta baldosa bicolor formada por la división de un cuadrado en dos triángulos por su diagonal es uno de los diseños tradicionales más antiguos que aún sigue vigente.
Ya está documentada a principios del siglo XVII con el nombre de baldosa mitadada. También es conocida con el nombre de baldosa de cartabón, baldosa de vela o baldosa de pañuelo.
La podemos encontrar por todas partes, bajo los balcones, en fachadas, tejados, escaleras, bancos, pavimentos o paredes. A veces llenando el espacio ella sola, a veces enmarcando figuras u otras alicatados.
Contrasta su sencillez de diseño con la versatilidad de diseños que se consiguen combinándolas. Este uno de los motivos de su popularidad e importancia patrimonial.
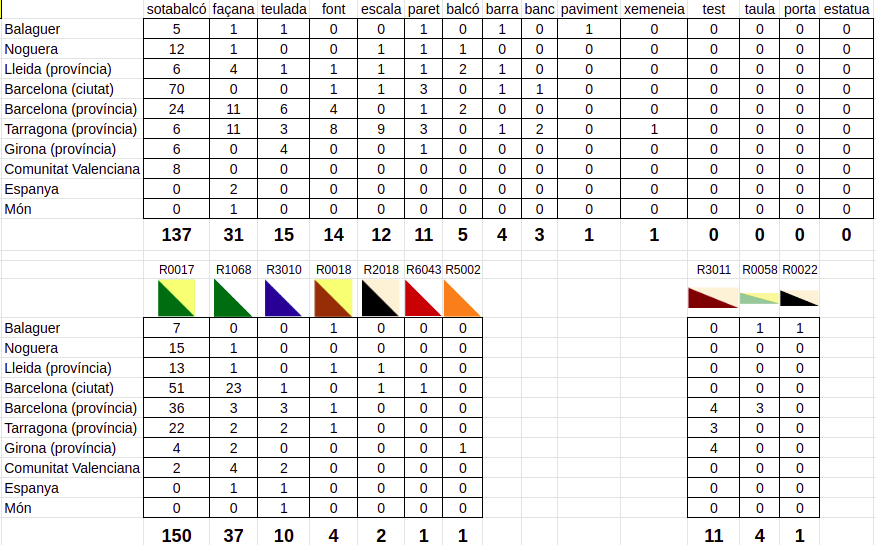
El compañero Ramon Tejedor (en twitter @Tejerauskas geoGebra tejerauskas), ha hecho una recopilación de localizaciones de la baldosa cartabón en Cataluña.
El document conté les ubicacions d’aquests més de 330 indrets, la gran majoria en l’espai públic. Podeu col·laborar-hi enviant-li noves localitzacions.
¿Cuántos diseños diferentes hay con estas 4 baldosas?
El espacio para 4 baldosas que hay entre los dos espejos, se puede llenar ni más ni menos que de 256 formas diferentes. Esto es por qué cada baldosa se puede poner con la flecha que forma el triángulo verde apuntando en 4 direcciones, con 4 baldosas tenemos 4*4*4*4 = 256

Si consideramos iguales los diseños que coinciden rodando el conjunto de las baldosas, hay que dividir por 4 esta cifra.
256/4 = 64
En la imagen se muestran 8 de estas 64 formas diferentes de poner 4 baldosas. A la derecha el friso(*) que se ve con los espejos paralelos.
(*) Tomando el nombre de friso como el elemento arquitectónico en forma de banda horizontal en las fachadas de los edificios, en matemáticas, un friso es un mosaico que se extiende en una sola dirección.

¿Se pueden hacer todos los frisos con estos dos espejos?
No, los espejos crean la repetición ninguneado simétricamente la imagen. Pero en el mundo físico real podemos no capear las baldosas, simplemente las podemos trasladar y así construir mosaicos sin simetría. Fijémonos en los frisos siguientes, no tienen ninguna simetría vertical. Comprueba cómo no se pueden hacer con los 2 espejos paralelos.
A diferencia de los frisos de la imagen anterior, en los que, si nos los imaginamos dibujados en una larga tira de papel, la podemos doblar de forma que el friso de un lado y otro coincidan, en estos frisos no hay forma en que doblando la tira de papel coincidan las figuras.

Sebastien Truchet
Sebastien Truchet (Lyon 1657–1729) fue un polifacético científico que estudió sistemáticamente los múltiples patrones que se pueden formar con esta baldosa. Es por ello que estos mosaicos son conocidos por los matemáticos y diseñadores con el nombre de truchet tiling
Enllaços a materials
- Proposta de treball a l'aula sobre mosaics de l'Anton Aubanell
- Segona proposta de treball a l'aula sobre mosaics de l'Anton Aubanell
- Proposta treball sobre la Rajola catalana a infantil de Toni Monclús
- Propostes de Núria Serra sobre tessel·lacions
- La construcció dels 7 frisos, una proposta d'Enric Brasó