Tota la informació dels nostres materials
A través del web volem facilitar les explicacions, les orientacions, les guies, les lectures, els contextos històrics, els suggeriments i les preguntes de cada mòdul. Estem elaborant material per cadascun dels mòduls i, a poc a poc, seguirem ampliant aquest apartat. Us animem a col·laborar en aquesta tasca de recopilació i documentació. Feu-nos arribar els comentaris i suggeriments.














Cercador
GEOMETRIA
Les corbes que s’obtenen fent rodar circumferències de diferent mida.
Les taules on utilitzant 4 miralls veiem tots els poliedres importants.
Mira les seccions dels objectes il·luminades pels leds vermells d’aquesta anella.
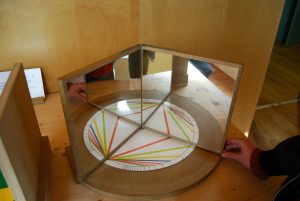
Varia l’angle dels miralls i crea així els diferents polígons.
Prova de posar el tetraedre i l’octaedre dins el cub.
Dues boles, una baixa en línia recta, l’altre fent corba. Quina arriba abans?
Posa els bastons blaus, perpendiculars a les arestes del dodecaedre per construir l’icosaedre.
Amb totes les peces construïm 3, 2 o 1 triangles equilàters
El con artesanal de fusta que mostra les seves seccions: Circumferència, el·lipse, paràbola i hipèrbola.
Amb les mateixes peces, reconstrueix dos polígons.
Sis caixes amb miralls interiors que permeten veure una varietat enorme de mosaics.
La vella coneguda taula de multiplicar, convertida en escultura.
Un enrajolat amb tessel·les en forma de sargantana ideades per l’artista M. Escher.
Múltiples formes de visualitzar i entendre aquest famós teorema
Un enrajolat no periòdic.
Construeix poliedres amb peces imantades.
Construeix aquest pont, sense cap subjecció, ideat per Leonardo
Com caben més cilindres?
En malla quadriculada o en malla triangular.
Aixequem aquests arcs amb coixins.
Una habitació sorprenent on la geometria fa canviar de mida les coses.
Taller on es construeixen aquestes estructures autosostenibles.
Com canvien les longituds, superfícies i volums d’objectes semblants?
Estratègia, combinatòria
Tres anelles per enllaçar-les d’una forma molt especial.
Visualitzant propietats numèriques amb cubs i altres peces.
Cal traslladar la torre movent els discs un a un i deixant sempre els petits sobre els grans.
Posa les peces de forma que els colors no estiguin de costat. És una versió del teorema dels 4 colors.
Fes tants conjunts diferents got-cullera-ganivet com sigui possible.
El puzle de reconstruir el tauler d’escacs que sembla difícil, però que l’organització el facilita.
Posa els gratacels tenint en compte quants es veuen des de cada posició.
Amb la cadeneta fem un recorregut que passi per tots els vèrtexs del dodecaedre
Posa les tanques dels corrals, les xifres indiquen la quantitat de tanques al seu voltant.
Col·locar les 16 peces sense que ni en files ni en columnes es repeteixin ni colors ni nombres.
Càlcul
Llistat de les pàgines de mòduls per ordre alfabètic
- 5 Triangles
- 6 segons
- Anamorfisme cilíndric
- Cadena calidoscòpica
- Caixa capgiradora
- Calidoscopi esfèric
- Calidoscopis polièdrics
- Camins de Hamilton al dodecaedre
- Camins girats
- Coberts i gots
- Coincidències
- Comptar pedres
- Corrals
- Daus enverinats
- Daus intransitius
- De 4 a 12
- De l’octaedre al cub
- Deu polígons amb simetries
- Desfés la suma
- Diagrama de Voronoi
- Disseccions de polígons
- Dodecaedre amb 3 miralls
- El bombo, les mostres i els intervals de confiança.
- El cercle de foc
- El con d’Apol·loni
- El cub SOMA
- El llibre de miralls
- El nombre d’or
- El nus borromeu
- El pentàgon atrapat
- El Polydron
- El pont de Leonardo
- El tauler d’escacs trencat de Sam Loyd
- Els barrets d’Einstein
- Els calidoscopis de mosaics plans
- Els quadrats grecollatins
- Empaquetar cilindres
- Encaixant poliedres
- Encaixar costats del mateix color
- Epicicloides i hipocicloides
- Factors primers
- Fórmules inductives
- Frisos amb miralls paral·lels
- Geocares
- Gratacels
- Impressió 3D
- Intersecció de polígons
- Inversor
- L’arc catenari i l’arc de mig punt
- L’atzar no és regular
- L’esfera de la Terra
- L’habitacio d’Ames
- L’home de Vitruvi
- La campana de Gauss
- La cicloide
- La corba de Hilbert
- La guardiola
- La lemniscata
- La loteria, un impost voluntari
- La paradoxa del bitllet
- La rajola de Can Mercader
- La taula de multiplicar 3D
- Laberint matemàgic
- Laberints
- Les cúpules de Leonardo
- Les sargantanes d’Escher
- Les torres de Hanoi
- Longitud, superfície i volum
- Maniobrant cotxes
- Matemàtica mesopotàmica
- Mirall amb polígons
- Mirall de lletres
- Mirall del pallasso
- Mirallet, mirallet
- Omplint cercles
- Ordenar caixes o no
- Paradoxa del quadrat
- Parelles
- Pintant la pilota
- Pitàgores
- Poliedres duals
- Posar fitxes numèriques al quadrat, cercle i triangle
- Puzle de fraccions
- Quadrat de quadrats
- Quadrat panda
- Quatre cubs de colors
- Qui és qui de fraccions
- Reptes de càlcul
- Semidesintegració
- Simetries de dos triangles
- Tangram
- Tangram egipci
- Teorema de l’amistat
- Tessel·lació de Penrose
- Tres possibilitats
- Tres triangles equilàters
- Triangles màgics
- Una suma d’infinits termes
- Vestir poliedres
Mòduls exposats a Cornellà per sales
Descobreix els mòduls de cada sala de l'exposició permanent de Cornellà "Experiències Matemàtiques"
Podeu descarregar el Catàleg de mòduls del MMACA (Realitzat el 2017) o veure els mòduls de cadascuna de les sales de l’exposició permanent “Experiències matemàtiques” de Cornellà.