Cuadrado panda

Coloca las 16 fichas en el marco cuadrado 4×4 de manera que los colores de los lados que se tocan coincidan.

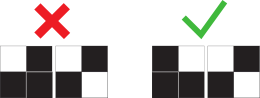
  • Ubicación:
  • Edad mínima: a partir de 6 años.
  • Tiempo requerido: 15 minutos.
  • Número de participantes: Una o más personas
  • Palabras clave: Rompecabezas, simetría, cuadrado
  • Taxonomía: Geometría, Combinatoria

Més reptes? Ajuda?

Las 16 piezas

Para construir las piezas se divide el cuadrado en 4 cuadrados iguales y se pintan de negro o blanco de todas las formas posibles diferentes. No se tienen en cuenta las rotaciones que harían algunas piezas iguales. 

Las soluciones

Hay muchas soluciones posibles, así que conseguir alguna es asequible. 

Normalmente, el proceso es ir llenando el marco con las piezas hasta que se detecta que ninguna de las piezas que restan se puede poner, entonces es el momento de reflexionar y recolocar alguna peca. 

Os animamos a compartir vuestra solución en las redes sociales con la etiqueta #pandasquare

#pandasquare

Ivan Moscovich, el gran iniciador de los museos científicos interactivos

Este rompecabezas aparece con el nombre de BITS en el libro de Ivan Moscovich "Super games"

Ivan Moscovich nació de padres judíos en Vojvodina (actual Servia) en 1926. A los 17 años fue internado en el campo de concentración de Auschwitz. Pasó por 4 campos de concentración y 2 campos de trabajo forzado.

Terminada la guerra estudió ingeniería mecánica en la Universidad de Belgrado y emigró a Israel donde trabajó como investigador científico implicado en el diseño de materiales didácticos, ayudas educativas y juegos educativos.

En 1964 fundó el Museo de Ciencia y Tecnología de Tel-Aviv. Este fue uno de los museos que cambió la forma expositiva tradicional, incorporando muchos materiales interactivos de ciencias, matemáticas y arte. Uno de sus visitantes fue el físico Frank Oppenheimer, las ideas, diseños y materiales que recogió fueron la semilla del revolucionario Exploratorium de San Francisco que Oppenheimer inauguró en 1969 y que aún hoy es un referente de los museos interactivos como el nuestro.

Ivan Moscovich a los 93 años. (fuente: jewishjournal.com)

Moscovich es un escritor incansable, tiene más de 30 libros en la web de Amazon, todos ellos recomendables, constituyen una fuente inestable de ideas originales.

Es también un gran creador de juegos como el mítico "Magic robot", "Magic mirror", "Tricky fingers", "30cubed" o "Fold"

magic-robot-game
magic_mirror
trick finders
30cube
folded

Investigaciones en torno a las soluciones

David Butler profesor del Centro de Aprendizaje de Matemáticas de la universidad de Adelaida (Australia) explica en su blog cómo en 2016 sacó la idea del libro de Ivan Moscovich y le puso el nombre de PANDA SQUARE. 

Es interesante la enumeración de las preguntas que plantea, algunas con respuesta, otras que aún quedan abiertas:

  • ¿Es posible alguna solución con algún tipo de simetría o rotación?  ¿Qué simetrías se pueden descartar?
  • ¿Cuántas soluciones hay?
  • A partir de una solución, ¿cuántas soluciones derivadas se pueden encontrar fácilmente?
  • ¿Es posible tener una solución donde todas las baldosas idénticas estén en una orientación diferente?
  • ¿Existe una solución con una sola región negra conectada?
  • Parece que en las soluciones encontradas siempre al menos una de las baldosas totalmente negras o totalmente blancas están en los bordes. ¿Se puede probar?
  • ¿Es posible que la baldosa totalmente negra esté en un borde y en el borde opuesto esté la baldosa totalmente blanca?
magic_mirror

En 2020, David Butler hizo un hilo explicando el hallazgo y demostración de las únicas 4 soluciones simétricas.