¿Cuál es la proporción de bolas de colores?
En aquest bombo transparent hi ha boletes de dos colors. Un llistó amb ranura permet recollir una mostra de 50 boletes. La proporció de boles de colors observada a la mostra, és una estimació de la proporció que ens demanen.
Fent lliscar una peça per tal que indiqui la proporció de la mostra, podem llegir l’interval de confiança del 95%, és a dir entre quins valors està la proporció de boles de color de tot el bombo.
- Ubicació en el museu: Sala Lluís Santaló
- Edad mínima: a partir de 12 años.
- Tiempo requerido: 5-10 minutos.
- Número de participantes: 1 o más si necesita ayuda para realizar los cálculos.



Funcionamiento general
Hay que hacer girar el bombo de manera que el listón de madera quede totalmente lleno, de esta forma se han seleccionado exactamente 50 setas.
Las 50 bolas en la barra son nuestra muestra aleatoria. Es necesario contar cuántas bolas azules hay. Si, por ejemplo, tenemos 8 bolas azules del total de 50, esto significa que el porcentaje de bolas azules en la muestra es del 16%. Este es un cálculo mental fácil de hacer.
Una vez tenemos el porcentaje de la muestra o proporción muestral, hemos pasado a la pieza de madera unida al tambor, su deslizador hasta que nos indique este valor. Luego podemos leer los valores mínimos y máximos que indica para una muestra de tamaño 50. Este es el intervalo de confianza donde se encuentra el porcentaje real de bolas de color, con una probabilidad del 95%.
Reflexionemos: El resultado es realmente un intervalo muy grande. Para ajustar más el resultado y obtener un intervalo de confianza más pequeño tenemos que trabajar con una muestra más grande. Podemos hacer esto con el mismo tambor. Recogemos 50 bolas y sumamos los resultados. El control deslizante ha especificado el intervalo de confianza para muestras de diferentes tamaños.
Conceptos relacionados
Contexto histórico
En 1937 ya existen publicaciones que desarrollan el concepto de intervalo de confianza. Sin embargo, tardó mucho tiempo en usarse de manera precisa y rutinaria. Por ejemplo, no fue hasta 1997 que un ensayo con un conjunto muy grande de muestras y un intervalo de confianza aceptable pudo garantizar que la terapia con cortisol no redujera el riesgo de accidente cerebrovascular agudo[fuente].
Comentarios
Sacar conclusiones sobre los datos de solo unas pocas muestras es un proceso al que estamos acostumbrados. Es necesario ser conscientes de que requiere que la característica que estudiamos se distribuya uniformemente a toda la población y que nos aseguremos de que al tomar la muestra todos los elementos tengan la misma probabilidad de ser elegidos.
Como anécdota, ilustrativa: en el proceso de construcción de este módulo tuvimos que descartar una cierta remesa de bolas de colores porque tenían un ligero agarre en las paredes del tambor.
Aplicaciones
A partir de las proporciones de la muestra es relativamente fácil aproximarse a las proporciones que se darán a toda la población sin la necesidad de muestrear a toda la población. Esto es muy útil cuando se trata de encontrar la prevalencia (proporción) de ciertas enfermedades en un país o incluso en todo el mundo. De esta manera se puede encontrar, por ejemplo, la proporción de fumadores en un país y hacer una previsión del gasto sanitario que representarán en el futuro.
Fácil reproducción de este módulo en el aula
Necesitamos una caja de metacrilato u otro material transparente y bolas bicolores de exactamente el mismo tamaño y características. Pueden ser perlas para hacer collares o pulseras o, como las de este módulo, proyectiles para escopetas de aire comprimido.
La caja debe llenarse aproximadamente a la mitad. y sellarlo con cinta adhesiva para que no se abra al remover.
Una vez lo hemos agitado podemos considerar que la muestra es la fila de bolas que se han situado a lo largo de uno de los bordes inferiores.
Simulación con una hoja de cálculo
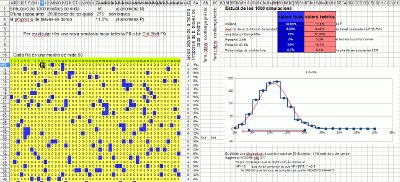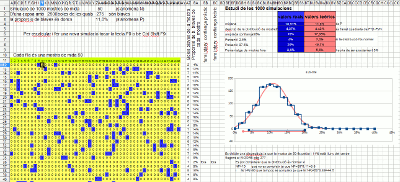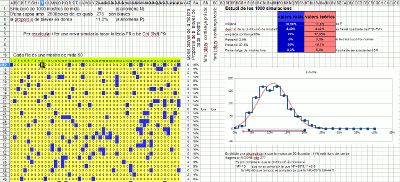
Las hojas de cálculo tienen la función que genera un número aleatorio entre 0 y 1, normalmente su sintaxis es =RAND(). También tienen una opción (generalmente F9) que recalcula toda la hoja y por lo tanto renueva todos estos valores. Esto se basa en esta hoja de cálculo (XLS, ODS) donde se simulan 1.000 extracciones de una muestra de tamaño 50. De estas 1.000 proporciones de muestra, se realiza un histograma (en azul) que se superpone con la curva normal correspondiente (en rojo). Comprueba que se ajusta correctamente y, por lo tanto, justifica el ancho del rango de confianza utilizado en el control deslizante.
