Observa los colores de las caras de los dados, de las 6 caras hay dos rojas, imagina que el rojo representa un veneno.
Tirando un solo dado, ¿qué es más probable que salga veneno o que no?
¿Y tirando los dos dados? ¿Qué es más probable envenenarse o no envenenarse?
Per enverinar-se n’hi ha prou que un dels daus surti vermell!
Estudio experimental
Puedes usar el ábaco como contador para descubrir estas probabilidades de forma empírica
- En el caso de un dado, las probabilidades de los dos casos difieren un 33%, así que rápidamente comprobarás que es más probable no envenenarse.
- En el caso de los dos dados, las dos probabilidades solo difieren un 11%, así que quizás tendrás que tirarlos más veces para comprobar que es más probable envenenarse.
Análisis de casos equiprobables
Podemos suponer los dados regulares y equilibrados, entonces al ser seis caras , la probabilidad de que queden de una cara determinada es 1/6 o del 16 ́6%
Con un dado, las probabilidades son 2/6 o el 33'3% de envenenarse y 4/6 o el 66 ́7% de no envenenarse.
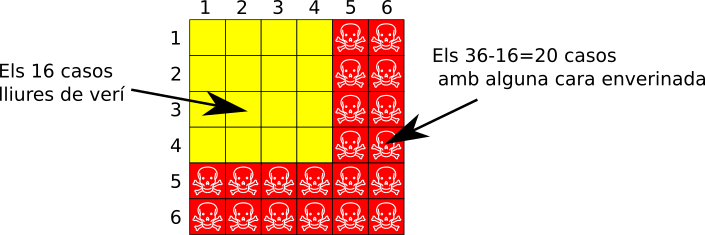
Con dos dados hay que distinguir cara por cara los dos dados, hay 6 x 6 = 36 casos diferentes equiprobables. Para calcular cuántos de estos casos tienen veneno, es más sencillo contar lo contrario: hay 4 caras sin veneno de un dado y 4 sin veneno del otro dado combinándolas salen 4×4=16 casos sin veneno. Todos los demás casos tienen o bien una cara con veneno o bien las dos, son 36-16=20 casos. Así que las probabilidades son 16/36 o 44 ́4% de no envenenarse y 20/36 o el 56% de envenenarse.
- Ubicación: Sala Lluís Santaló
- Edad mínima: a partir de 10 años.
- Tiempo requerido: 5 minutos.
- Número de participantes: Una o más personas
- Palabras clave: Azar, frecuencia probabilidad.
- Taxonomía: Probabilidad y estadística

