Daus enverinats - Museu de Matemàtiques de Catalunya

Look at the colors of the faces of the dice, of the 6 faces there are two red, imagine that red represents a poison.

Throwing a single dice, what is more likely to come out poison or not?

And throwing the two dice? What is more likely to be poisoned or not poisoned?

Per enverinar-se n’hi ha prou que un dels daus surti vermell!

Experimental study

You can use the abacus as a counter to discover these probabilities empirically

In the case of a die, the probabilities of both cases differ by 33%, so you will quickly find that it is more likely not to be poisoned.
In the case of both dice, the two probabilities differ only by 11%, so you may have to throw them away more times to verify that it is more likely to poison yourself.

Analysis of equiprobable cases

We can assume the regular and balanced dice, then since they have six faces , the probability that they remain of a certain face is 1/6 or 16 ́6%

With a die, the odds are 2/6 or 33.3% of poisoning and 4/6 or 66'7% of not being poisoned.

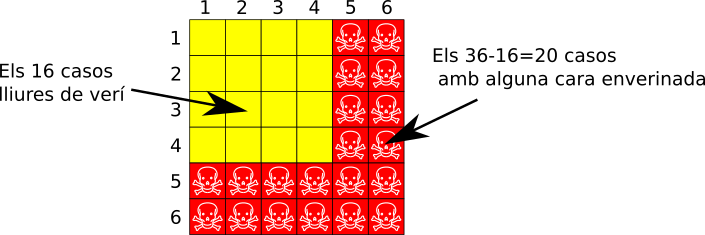
With two dice it is necessary to distinguish face by face the two dice, there are 6 x 6 = 36 different cases equiprobable. To calculate how many of these cases have poison, it is easier to count the opposite: there are 4 faces without poison from one die and 4 without poison from the other die combining them come out 4×4 = 16 cases without poison. All other cases have either a face with poison or both, they are 36-16=20 cases. So the odds are 16/36 or 44'4% of not getting poisoned and 20/36 or 56% of poisoning.