Gira la rueda para que todas las boletas queden en el depósito, entonces volviéndola a girar para que se distribuyan entre las columnas. Antes de hacerlo: ¿Puedes prever cómo quedará?
Efectivamente, no todas las barras se llenan igual, esta silueta donde las barras centrales son más altas que las laterales que recuerda la forma de campana y se llama campana de Gauss.
Esta forma de campana con los valores centrales más repetidos y una disminución progresiva a ambos lados, aparece a menudo midiendo objetos o fenómenos naturales. A veces el mismo desgaste indica la frecuencia de uso y crea de forma natural la forma acampanada.
- Ubicación: Sala Lluís Santaló
- Edad mínima: a partir de 6 años.
- Tiempo requerido: 5 minutos.
- Número de participantes: Una o más personas
- Palabras clave: Galton, Gauss distribución normal,
- Taxonomía: Probabilidad y estadística

¿Por qué se llenan las columnas de esta manera?
Si el aparato solo tuviera menos bifurcación y solo 3 barras para recoger las bolitas, ¿cómo se llenaría?
Piénsalo antes de pasar el ratón por encima de la imagen para descubrirlo
Efectivamente, en la primera bifurcación las boletas se reparten por igual: la mitad por un lado y mitad por el otro (en proporción 1-1).
En la siguiente bifurcación se vuelven a dividir, una cuarta parte de las boletas por cada camino, pero como los dos caminos centrales se juntan la proporción es 1-2-1
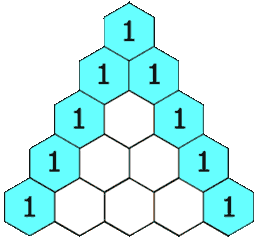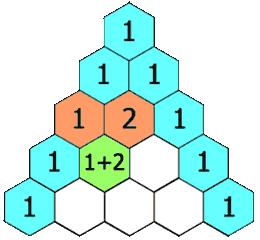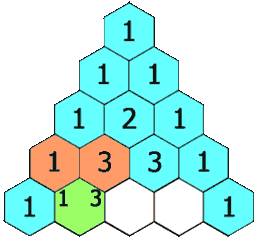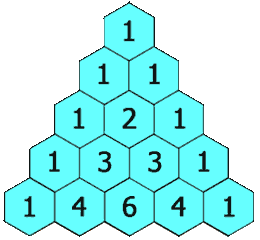
Lo mismo ocurre por las siguientes bifurcaciones, las sucesivas proporciones están indicadas con rojo en la imagen, forman el conocido como Triángulo de Tartaglia.
Este conocido triángulo con múltiples propiedades se forma sumando los dos números de la fila superior.
En este aparato concreto con 8 niveles de bifurcaciones, las alturas de las barras de boletas se aproximan a las probabilidades teóricas:
1/ 256, 8/256, 28/256, 56/256, 70/256, 56/256, 28/256, 8/256, 1/ 256
Se trata de la distribución binomial con n=8 y p=0.5 dibujada en azul.
Al ir aumentando las bifurcaciones esta distribución discreta se aproxima a la distribución continua llamada normal o gaussiana dibujada en verde en la imagen

Carl Friedrich Gauss
Johann Carl Friedrich Gauss (1777-1855), fue uno de los matemáticos más influyentes de la historia, es llamado "Príncipe de los matemáticos". En cualquier especialidad de la matemática actual se puede encontrar algún concepto o resultado importante que lleva su nombre.
Su gran obra Disquisitiones arithmeticae, ha sido traducida y publicada al catalán por el IEC.
También podéis encontrar una interesante biografía novelada suya titulada "El hombre de la campana" escrita por Joan Girbau en 2015.

Imagen de la Viquipedia
Francis Galton
Francis Galton (1822-1911), inventor de este aparato, era primo de Charles Darwin, fue un influyente y polifacético científico que trabajó sobre meteorología, antropología, herencia, estadística, antropometría, biología del desarrollo y también psicología.
Es un ejemplo de la influencia de la ideología sobre las teorías científicas. Elaboró el término eugenesia que defiende la existencia de personas y grupos superiores e inferiores y estudia formas de "mejorar" la calidad genética humana. Esta teoría fue la base sobre la que se fundamentó las políticas de limpieza étnica y social que se aplicaron no solo en la Alemania nazi también en Estados Unidos, Canadá, Suecia, Suiza o Australia.
Galton invirtió todo su dinero y capacidades en medir y cuantificar las características humanas para justificar su teoría, desarrollando para ello herramientas estadísticas hoy valiosas.
Con ojos actuales, es ciertamente una parte incómoda de la historia de la estadística.

Imagen de la Viquipedia



