Rotate the wheel so that all the balls remain in the tank, then rotate it again so that they are distributed between the columns. Before doing so: Can you predict what it will look like?
Indeed, not all bars are filled equally, this silhouette where the central bars are taller than the sides reminiscent of the bell shape and is called the Gauss bell.
This bell shape with the most repeated central values and a progressive decrease on both sides, often appears measuring natural objects or phenomena. Sometimes the same wear indicates the frequency of use and naturally creates the flared shape.
- Hotel Area: Sala Lluís Santaló
- Minimum age: from 6 years old.
- Required time: 5 minutes.
- Number of participants: One or more people
- Keywords: Galton, Gauss normal distribution,
- Taxonomy: Probability and statistics

Why are columns filled in this way?
If the device only had less fork and only 3 bars to collect the balls, how would it be filled?
Think about it before hovering your mouse over the image to find out
Indeed, at the first fork the balls are distributed equally: half on one side and half on the other (in a 1-1 ratio).
At the next fork they are divided again, a quarter of the balls for each path, but since the two central paths are joined together the ratio is 1-2-1
The same goes for the following forks, the successive proportions are indicated with red in the image, they form what is known as the Tartaglia Triangle.
This well-known triangle with multiple properties is formed by adding the two numbers in the upper row.
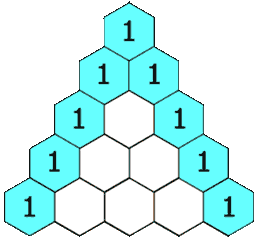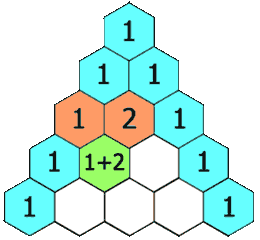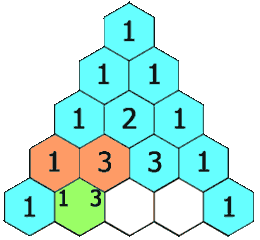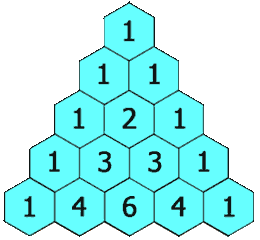
In this particular apparatus with 8 levels of forks, the heights of the ball bars approach the theoretical probabilities:
1/ 256, 8/256, 28/256, 56/256, 70/256, 56/256, 28/256, 8/256, 1/ 256
This is the binomial distribution with n=8 and p=0.5 drawn in blue.
As the forks increase, this discrete distribution approaches the continuous distribution called normal or Gaussian drawn in green in the image

Carl Friedrich Gauss
Johann Carl Friedrich Gauss (1777-1855), one of the most influential mathematicians in history, is called "Prince of mathematicians". In any specialty of current mathematics you can find some important concept or result that bears his name.
His great work Disquisitiones arithmeticae, has been translated and published into Catalan by the IEC.
You can also find an interesting biography of his novel entitled "The Man with the Bell" written by Joan Girbau in 2015.
Francis Galton
Francis Galton (1822-1911), inventor of this device, was a cousin of Charles Darwin, was an influential and multifaceted scientist who worked on meteorology, anthropology, inheritance, statistics, anthropometry, developmental biology and also psychology.
It is an example of the influence of ideology on scientific theories. He developed the term eugenics that defends the existence of higher and lower people and groups and studies ways to "improve" human genetic quality. This theory was the basis on which the policies of ethnic and social cleansing were based, which were applied not only to Nazi Germany but also to the United States, Canada, Sweden, Switzerland and Australia.
Galton invested all his money and capabilities in measuring and quantifying human characteristics to justify his theory, thereby developing statistical tools that are now valuable.
With current eyes, it is certainly an awkward part of the history of statistics.





