Coloca los cuadrados de manera que rellenen el marco.
Amb 11 quadrats formar un quadrat
En 1907, Sam Loyd propuso este rompecabezas:
La Sra. Perkins recibió un cubrecamas hecho con 169 cuadrados de seda. ¿Cómo se puede dividir en el menor número posible de piezas cuadradas?
Aquí, las piezas ya están hechas, son 11 cuadrados de lados 1,1,2,2,2,3,3,4,6,6 y 7 con los que se puede reconstruir un cuadrado de lado 13. Intenta hacerlo.
Amb 9 quadrats formar un rectangle
Esta es una versión en la que el objetivo es reconstruir un rectángulo de lados 32 y 33 con nueve piezas cuadradas de lados 18,15,14,10,9,8,7,4 y 1
Intenta recomponer el cuadrado.
Teniu la solució a la portada del Scientific American que hi ha una mica més avall.
Una altra descomposició:

Aquesta és la descomposició del rectangle de 69×61 amb 9 quadrats de costats 2, 5, 7, 9, 16, 25, 28, 33 i 36
- Ubicació: sala Martin Gardner
- Edad mínima: a partir de 10 años.
- Tiempo requerido: 5-10 minutos.
- Número de participantes: Una o más personas
- Paraules clau: Combinatòria, quadrat, rectangle
- Taxonomia: Combinatòria, aritmètica
Soluciones
Amb 11 peces un quadrat de costat 13

Amb 9 peces un rectangle 32x33
Esta disección fue publicada en 1925 por Zbigniew Moroń.
En 1958 Martin Gardner en su columna en el Scientific American hizo mención.

La mínima disección PERFECTO del cuadrado
El cuadrado formado por 11 cuadrados de este módulo tiene piezas repetidas. Es una buena solución del problema de descomponer el cuadrado en cuadrados, pero no es la mínima, ya que hay una forma muy evidente de dividir un cuadrado en 4 cuadrados iguales. Si piensas un momento seguro que la encontrarás.
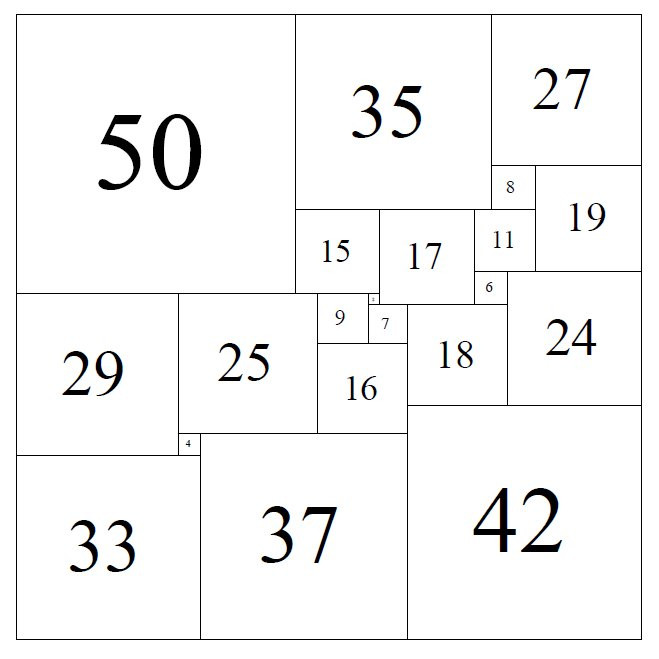
Así que desde 1930, se inició la búsqueda de la descomposición de un cuadrado en cuadrados diferentes con el mínimo número de piezas, el conocido como disección PERFECTO del cuadrado.
Tras sucesivos descubrimientos de disecciones perfectas con 55, 38, 26 y 25 cuadrados, En 1978 AJW Duijvestij encontró la descomposición en 21 cuadrados que muestra la imagen de la derecha. Al año siguiente Paul Leeuw demostró que no había otro con menos piezas.