Place the squares so that they fill the frame.
Amb 11 quadrats formar un quadrat
In 1907, Sam Loyd proposed this puzzle:
Ms. Perkins received a bedspread made of 169 squares of silk. How can it be divided into as few square pieces as possible?
Here, the pieces are already made, there are 11 squares of sides 1,1,2,2,2,3,3,4,6,6 and 7 with which you can reconstruct a square side 13. Try to do it.
Amb 9 quadrats formar un rectangle
This is a version in which the objective is to reconstruct a rectangle of sides 32 and 33 with nine square pieces of sides 18,15,14,10,9,8,7,4 and 1
Try to rebuild the square.
Teniu la solució a la portada del Scientific American que hi ha una mica més avall.
Una altra descomposició:

Aquesta és la descomposició del rectangle de 69×61 amb 9 quadrats de costats 2, 5, 7, 9, 16, 25, 28, 33 i 36
- Ubicació: sala Martin Gardner
- Minimum age: from 10 years old.
- Required time: 5-10 minutes.
- Number of participants: One or more people
- Paraules clau: Combinatòria, quadrat, rectangle
- Taxonomia: Combinatòria, aritmètica
Solutions
Amb 11 peces un quadrat de costat 13

Amb 9 peces un rectangle 32x33
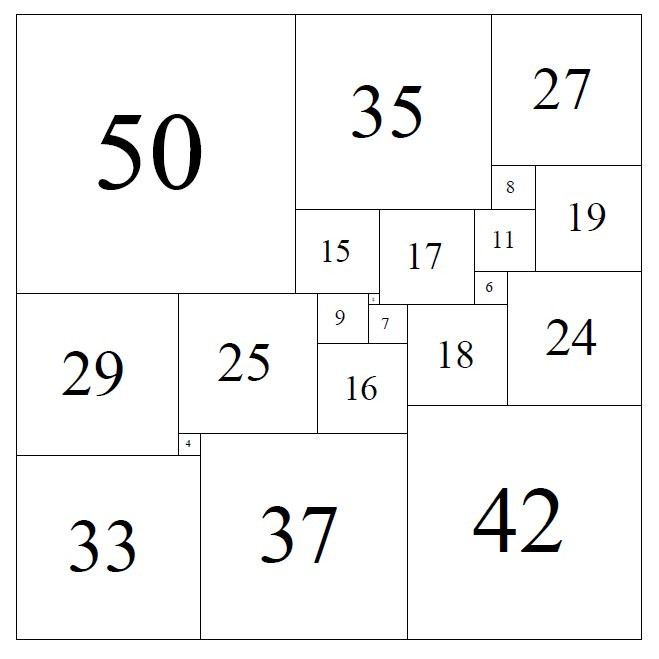
This dissection was published in 1925 by Zbigniew Moroń.
In 1958 Martin Gardner mentioned it in his column in Scientific American.

The minimum perfect dissection of the square
The square consisting of 11 squares of this module has repeated pieces. It is a good solution to the problem of breaking down the square into squares, but it is not the minimum, since there is a very obvious way to divide a square into 4 equal squares. If you think for a moment you'll surely find it.
So since 1930, the search for the decomposition of a square in different squares began with the minimum number of pieces, known as the PERFECT dissection of the square.
After successive discoveries of perfect dissections with 55, 38, 26 and 25 squares, in 1978 AJW Duijvestij found the decomposition in 21 squares showing the image on the right. The following year Paul Leeuw showed that there were no other pieces.