Aprovecha las simetrías de los poliedros para verlos a través de los espejos.
Pone las piezas horizontalmente, sostenidas a ambos lados.
Empieza por las piezas que son una sola barra.
Todas las piezas tienen una posición determinada en que encajan con los espejos. Buscala
¿Qué poliedro ves? Localizalo en el cartel.
Saca las piezas antes de poner otra
¿Qué ángulos forman los espejos?
Las tres tablas que forman este módulo tienen los 4 espejos dispuestos de forma que los ángulos entre ellos (ángulos diédricos) producen que los objetos se visualicen 3, 4 o 5 veces.
- El primer calidoscopio tiene los 4 ángulos diedros entre los espejos de 120º. Como cada ángulo triplica los objetos lo llamamos 3-3-3-3. Con esta disposición un simple objeto alargado colocado en el interior se visualiza como un tetraedro regular.
- Los diedros del segundo calidoscopio son de 120º, 90º, 120º y 90º. Lo llamamos 3-4-3-4. Permite visualizar el cubo y el octaedro regular.
- En el tercer calidoscopio los ángulos son 120º, 72º, 120º y 72º Lo llamamos 3-5-3-5. Permite visualizar el icosaedro y el dodecaedro regulares.
Además, en cada calidoscopio, un conjunto de piezas especiales permiten obtener los diferentes truncamientos. Se consiguen ver más de 25 poliedros diferentes.
- Ubicación: Sala Emma Castelnuovo
- Edad mínima: a partir de 10 años.
- Tiempo requerido: 5-10 minutos.
- Número de participantes: Una o más personas
- Palabras clave: simetrías, calidoscopios, espejos, poliedros.
- Taxonomía: GEOMETRÍA































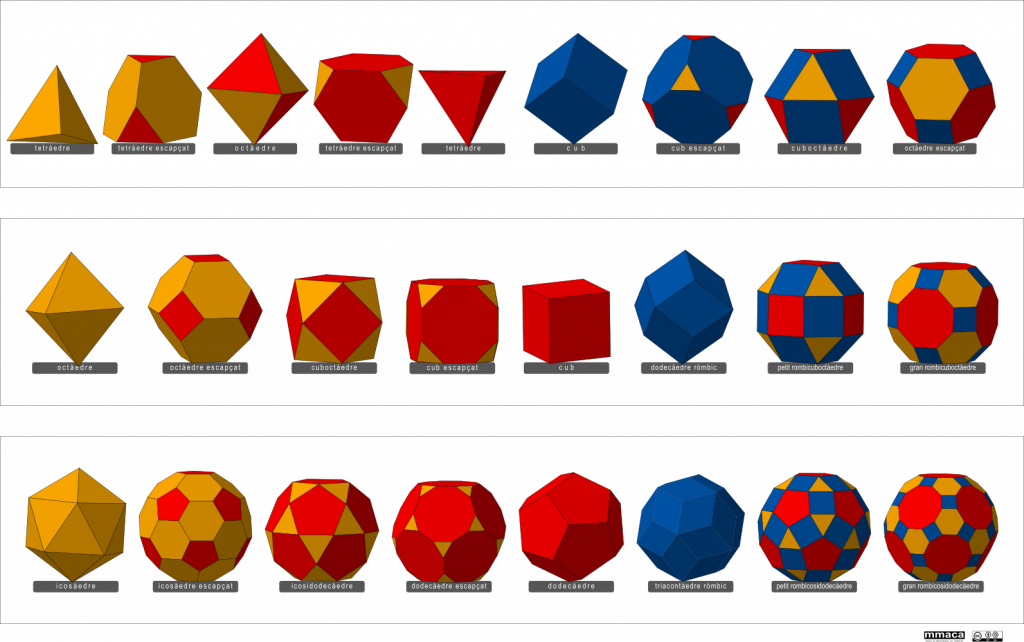
Los principales poliedros que se pueden visualizar con los calidoscopios 3-3-3-3, 3-4-3-4 y 3-5-3-5
Enlaces externos y material descargable
- Cartel con los poliedros que se pueden visualizar en las mesas de calidoscopios.
- Artículo de Josep Rey y Manel Udina en la revista NouBiaix sobre caleidoscopios y poliedros
- Notas para trabajar los módulos de esta sala preparados por Toni Gomà y Daniel Bosch
- Página "Polyhedral_kaleidoscopes" de la mathcom.wiki
