Take advantage of the symmetries of the polyhedra to see them through the mirrors.
Lay the pieces horizontally, held on both sides.
Start with the pieces that are a single bar.
All parts have a certain position in which they fit with the mirrors. Look for it
What polyhedron do you see? Find it on the poster.
Remove the pieces before putting on another one
What angles form the mirrors?
The three tables that make up this module have the 4 mirrors arranged so that the angles between them (dihedral angles) produce that the objects are visualized 3, 4 or 5 times.
- The first kaleidoscope has the 4 angles between the 120º mirrors. Since each angle triples the objects we call it 3-3-3-3. With this arrangement a simple elongated object placed inside is visualized as a regular tetrahedron.
- The second kaleidoscope is 120º, 90º, 120º and 90º. We call it 3-4-3-4. It allows you to visualize the regular cube and octahedron.
- In the third kaleidoscope the angles are 120º, 72º, 120º and 72º We call it 3-5-3-5. It allows you to visualize the regular icosahedron and dodecahedron.
In addition, in each kaleidoscope, a set of special pieces allows you to obtain the different truncations. You get to see more than 25 different polyhedra.
- Hotel Area: Sala Emma Castelnuovo
- Minimum age: from 10 years old.
- Required time: 5-10 minutes.
- Number of participants: One or more people
- Keywords: symmetries, kaleidoscopes, mirrors, polyhedra.
- Taxonomy: GEOMETRY































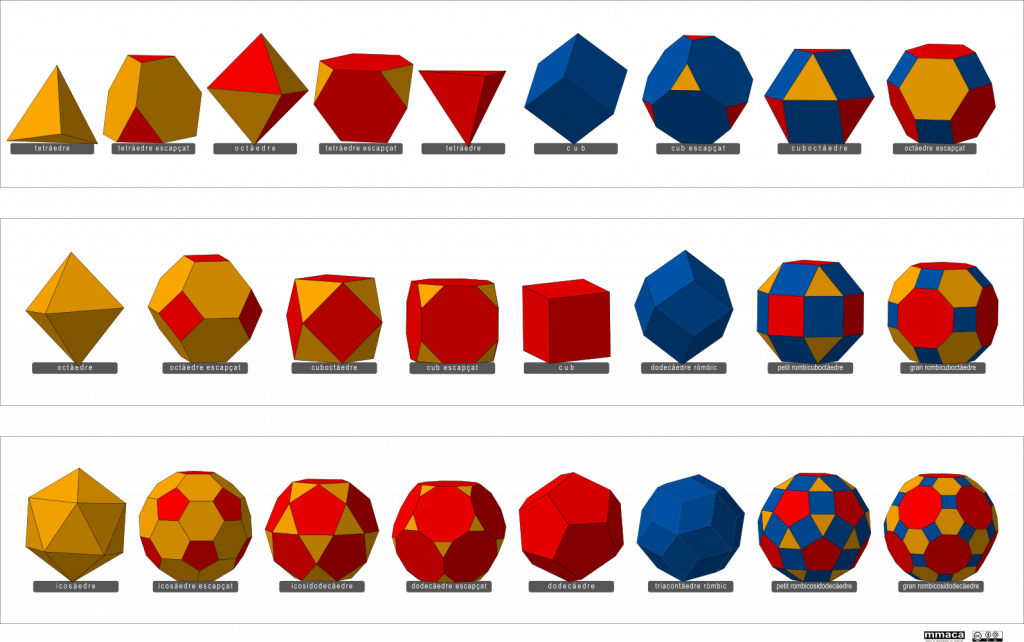
The main polyhedra that can be visualized with kaleidoscopes 3-3-3-3, 3-4-3-4 and 3-5-3-5
