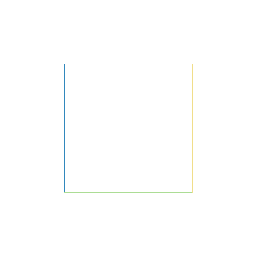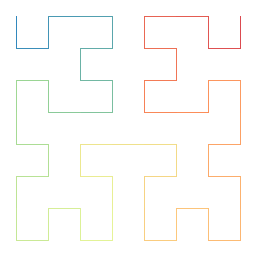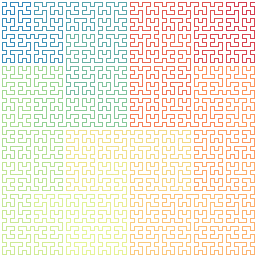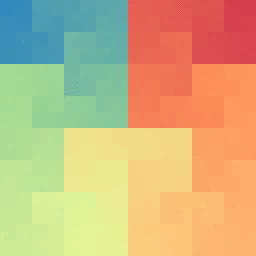Utilizando las 64 piezas iguales construye un cubo de 4x4x4 que tenga un camino continuo y cerrado.

- Ubicación: Sala Martin Gardner
- Edad mínima: a partir de 5 años.
- Tiempo requerido: 5-10 minutos.
- Número de participantes: Una o más personas
- Palabras clave: fractal, curva, recubrimiento
- Taxonomía: Modelos, patrones, fractales
La curva de Hilbert es un fractal
Esta curva fue descrita en 1891 por el matemático alemán David Hilbert como curva que recubre el llano.
Tal y como muestra la imagen, se inicia dividiendo un cuadrado en 4 cuadrados iguales y uniendo sus centros con una curva en forma U. El siguiente paso consiste en volver a dividir cada cuadrado en cuatro partes y en unir sus centros en una curva en forma de U que enlace con la siguiente.
La imagen muestra la octava iteración, repitiendo el procedimiento indefinidamente la curva acaba pasando por todos los puntos del plano.
El módulo muestra una generalización de la curva de Hilbert del llano a espacio tridimensional.
Aplicaciones
La forma sinuosa que tiene esta curva de recubrir el plano, o el espacio genera una buena y útil correspondencia entre un objeto de dimensión 1 (la curva) que podemos recorrer paso a paso y un objeto de dimensión 2 (el plano).
Esto se utiliza por ejemplo en el tratamiento digital de imágenes. Según qué modificación que haya que hacer en cada píxel, es mejor hacerlo siguiendo el recorrido de la curva de Hilbert en lugar de hacerlo fila en fila. La razón es que siguiendo el recorrido de Hilbert los píxeles cercanos a la lista corresponden siempre a píxeles cercanos a la imagen mientras que si lo hacemos por filas, el píxel inicial de cada fila va justo después del píxel final de la fila anterior aunque están muy distanciados a la imagen.