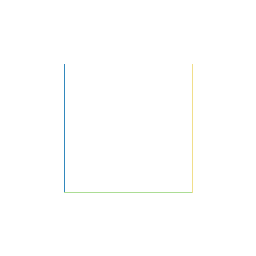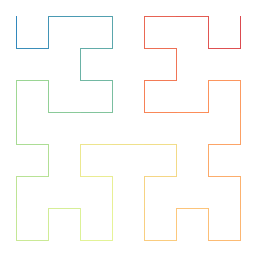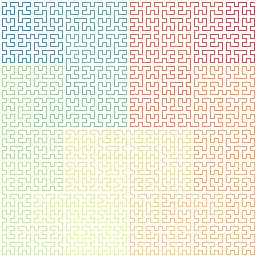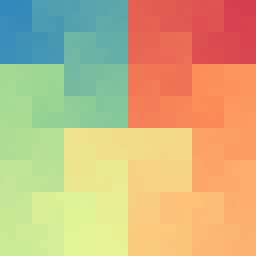Using the 64 equal pieces builds a 4x4x4 cube that has a continuous and closed path.

- Hotel Area: Sala Martin Gardner
- Minimum age: from 5 years old.
- Required time: 5-10 minutes.
- Number of participants: One or more people
- Keywords: fractal, curve, coating
- Taxonomy: Models, patterns, fractals
Hilbert's curve is a fractal
This curve was described in 1891 by the German mathematician David Hilbert as a curve covering the plane.
As the image shows, it begins by dividing a square into 4 equal squares and joining its centers with a U-shaped curve.
The image shows the eighth iteration, repeating the procedure indefinitely the curve ends up going through all the points of the plane.
The module shows a generalization of the Hilbert curve of the plane to three-dimensional space.
Applications
The winding shape of this curve of coating the plane, or space generates a good and useful correspondence between an object of dimension 1 (the curve) that we can go step by step and an object of dimension 2 (the plane).
This is used for example in digital image processing. Depending on what modification needs to be made to each pixel, it is better to do this by following the path of the Hilbert curve rather than row by row. The reason is that following Hilbert's path, the pixels close to the list always correspond to pixels close to the image while if we do it by rows, the initial pixel of each row goes just after the final pixel of the previous row although they are very distant to the image.