Con las mismas piezas reconstruye los dos polígonos.
En esta mesa verás diferentes rompecabezas. El objetivo es, con cada conjunto de piezas, formar los dos polígonos dibujados.
- Ubicación: Sala Puig Adam
- Edad mínima: a partir de 6 años.
- Tiempo requerido: 5-10 minutos.
- Número de participantes: Una o más personas
- Palabras clave: geometría, rompecabezas
- Taxonomía: GEOMETRÍA


El rompecabezas del mercader de ropa de Dudeney
En el libro "The Canterbury Puzzles, and Other Curious Problems" de 1907, el matemático Henry Ernest Dudeney propone el siguiente problema:
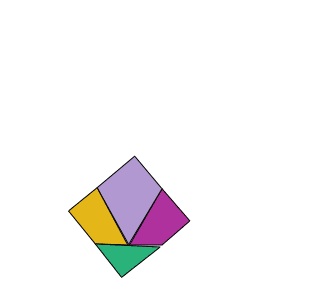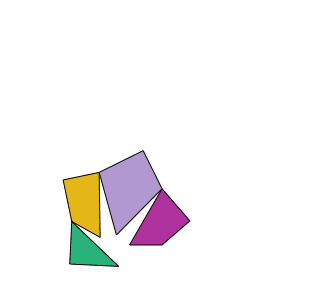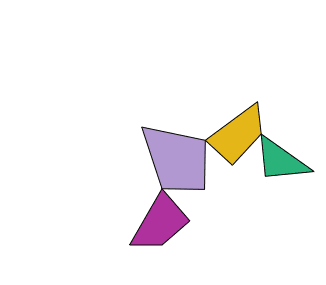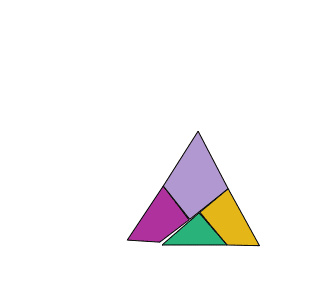
Se trata de cortar una prenda en forma de triángulo equilátero en cuatro trozos para hacer un cuadrado.
La solución es particularmente interesante, ya que las piezas se pueden articular para formar los dos polígonos como muestra la animación.

El caso general
El rompecabezas de transformar un triángulo en cuadrado y los otros de esta tabla son casos particulares de un resultado matemático más general:
Dados dos polígonos cualesquiera de la misma área, siempre existe una disección en un número finito de piezas que permite, reorganizándolas, formar cada uno de los dos polígonos.
Es el teorema de Wallace–Bolyai–Gerwien, llamado así por qué fue demostrado, de forma independiente, por estos tres matemáticos.
El teorema dice que la disección existe, pero no dice cómo hacerla ni en cuántas piezas hay que cortar. La forma de hacerlo, es diferente en cada caso. A menudo se ha descubierto más de una forma de hacerlo, sin embargo, las más interesantes son las que utilizan menos piezas. Esta página recoge las disecciones con menos piezas conocidas.
El hecho de que, siempre exista, una disección para cualquier pareja de polígonos con la misma área, puede parecer una cosa muy obvia, pero sorprendentemente, la cuestión análoga a dimensión tres tiene una respuesta negativa. Dados dos poliedros con el mismo volumen, no siempre es posible hacer una disección en piezas de un poliedro que permitan reconstruir el otro.
Las disecciones de la tienda del MMACA
En la tienda del MMACA encontraréis estas diferentes disecciones fabricadas por nosotros.
Otros módulos
En este módulo las circunferencias de diferentes tamaños pueden rodar sobre otro fijo, los engranajes permiten hacerlo sin resbalar. Las curvas obtenidas son hipocicloides (si se enrollan en el interior) e hipocicloides (si se enrollan por fuera). Dependiendo de los tamaños relativos de la circunferencia fija y de la que rueda, se obtienen los diferentes tipos de estas curvas.
Las 5 piezas de madera de diferentes tonalidades con las que se construye este cono muestran los 4 tipos de secciones: Circunferencia, elipse, parábola e hipérbola.
La primera parte consiste en un engranaje de 50 dientes en cuyo interior se puede girar un círculo de 25 dientes, los 5 puntos de color del círculo siguen los 5 diámetros. La segunda parte es una pieza pentagonal con los 5 vértices de color situados en la misma posición que antes. El pentágono puede girar suavemente gracias a los cordones insertados en las trincheras construidas como los diámetros de la primera parte.




