With the same pieces he reconstructs the two polygons.
In this table you will see different puzzles. The objective is, with each set of pieces, to form the two drawn polygons.
- Hotel Area: Sala Puig Adam
- Minimum age: from 6 years old.
- Required time: 5-10 minutes.
- Number of participants: One or more people
- Keywords: geometry, puzzle
- Taxonomy: GEOMETRY


The Dudeney Clothing Merchant Puzzle
In the 1907 book "The Canterbury Puzzles, and Other Curious Problems," the mathematician Henry Ernest Dudeney proposes the following problem:
It is about cutting a piece of clothing in the form of an equilateral triangle into four pieces to make a square.
The solution is particularly interesting, since the pieces can be articulated to form the two polygons as shown by the animation.

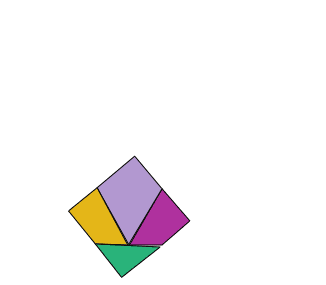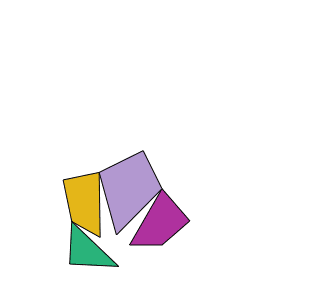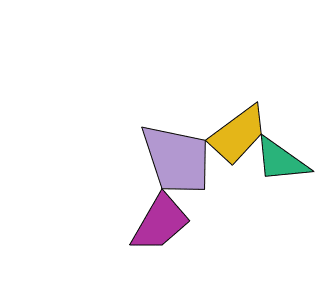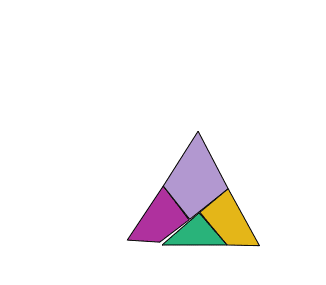
The general case
The puzzle of transforming a triangle into a square and the others in this table are particular cases of a more general mathematical result:
Given two polygons of the same area, there is always a dissection in a finite number of pieces that allows, reorganizing them, to form each of the two polygons.
It is wallace–Bolyai–Gerwien's theorem, named after why it was independently demonstrated by these three mathematicians.
The theorem says that dissection exists, but does not say how to make it or how many pieces to cut. The way to do it is different in each case. More than one way to do this has often been discovered, however, the most interesting are those that use the least pieces. This page contains the dissections with fewer known pieces.
The fact that there is always a dissection for any pair of polygons with the same area may seem like something very obvious, but surprisingly, the question analogous to dimension three has a negative response. Given two polyhedres with the same volume, it is not always possible to make a dissection in pieces of a polyhedrh that allow the other to be reconstructed.
The dissections of the MMACA store
In the MMACA store you will find these different dissections manufactured by us.
Other Modules
In this module the circumferences of different sizes can roll on another fixed, the gears allow to do it without slipping. The curves obtained are hypocycloids (if rolled inside) and hypocycloids (if rolled on the outside). Depending on the relative sizes of the fixed circumference and the one that rolls, the different types of these curves are obtained.
The 5 pieces of wood of different shades with which this cone is built show the 4 types of sections: Circumference, ellipse, parabola and hyperbola.
The first part consists of a gear of 50 teeth inside which can rotate a circle of 25 teeth, the 5 color points of the circle follow the 5 diameters. The second part is a pentagonal piece with the 5 color vertices located in the same position as before. The pentagon can rotate gently thanks to the laces inserted in the trenches built as the diameters of the first part.




