La sucesión de Fibonacci. El nombre auri Φ

- Ubicación: Sala George Polya
- Edad mínima: a partir de 10 años.
- Tiempo requerido: 5 minutos.
- Número de participantes: Una o más personas
- Palabras clave: arte, filotaxis
- Taxonomía: GEOMETRÍA
Leonardo de Pisa (1170-1250) es conocido como Fibonacci. Sus viajes comerciales al norte de África lo motivaron a traer a Europa el sistema de numeración hidu-arábigo. En su Liber apenas encontramos el problema:
"Un hombre puso una pareja de conejos rodeados por todos los lugares por una pared. ¿Cuántas parejas de conejos se pueden producir de esa pareja durante un año si se supone que cada mes cada pareja engendra una nueva pareja y que solo se pueden reproducir desde el segundo mes?"
Este problema se puede resolver con este esquema donde cada círculo significa una pareja de conejos, en azul pareja nueva y en rojo cuando se puede reproducir. Cada columna representa un mes. El número de parejas que tenemos cada mes es la sucesión de Fibonacci.
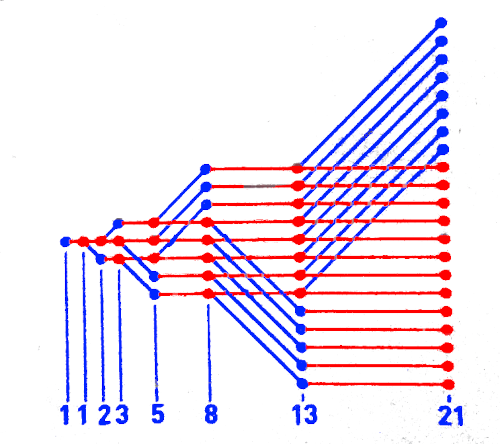
La sucesión de Fibonacci se obtiene de manera recursiva. Se inicia con un 1 en los dos primeros términos, a partir de ahí cada término se obtiene como la suma de los dos anteriores.
1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, 8+13=21, 13+21=34 ...
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, ...
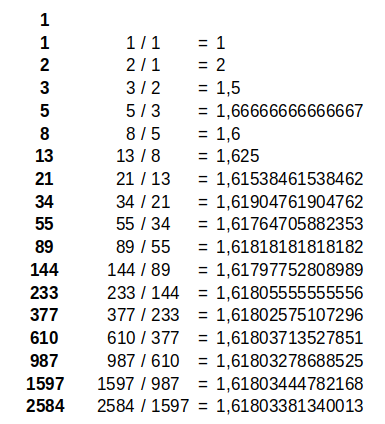
Si para ver la proporción del crecimiento del número de parejas de conejos mes a mes, dividimos las de un mes por las del mes anterior, obtenemos resultados diferentes, pero cada vez se asemejan más y tienden al número de oro Φ. Este es un número irracional cuya expresión en el sistema decimal tiene infinitas cifras que no se repiten periódicamente.
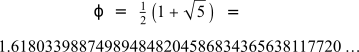
La margarita
Con este módulo se puede experimentar como el número de oro presente en la naturaleza.
La margarita es una flor compuesta. Lo que en una flor simple serían los pétalos, están en la margarita flores exteriores que hacen de pétalos, se llaman lígulas.
Las lígulas no están repartidas simétricamente e incluso se ven desordenadas. Puede parecer que están repartidas caóticamente, pero de hecho la posición donde van naciendo es la más eficiente para que no se tapen unas con las otras.
En el módulo se ve una margarita con las lígulas numeradas de manera que la número 1 es la más alejada o antigua y la 13 es la más cercana o reciente. Se puede experimentar como haciendo deslizar el arco auri (de 137,5º) alrededor de la margarita se va de una lígula a la siguiente.

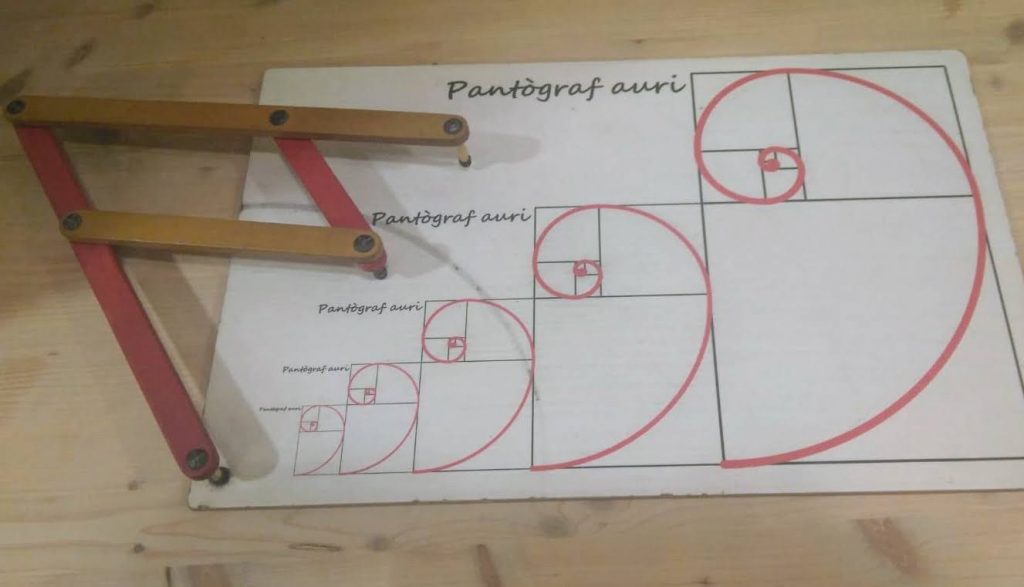
Pantógrafo auri
Un pantógrafo es un instrumento de dibujo que sirve para copiar dibujos a escala.
En los pantógrafos reales, la escala se puede ajustar cambiando la longitud de los brazos y los puntos de conexión. En este pantógrafo la escala está ajustada a 1:Φ , funciona como un compás auri.
Además los dibujos son espirales áureas, recorriendo con un brazo una espiral, el otro brazo si tuviera un lápiz pegado, dibujaría la otra espiral.
Rectángulos de Fibonacci
Si disponemos los rectángulos con lados los números consecutivos de la sucesión de Fibonacci de forma que coincidan en el vértice inferior, veremos cómo su diagonal se aproxima a una de las dos rectas dibujadas.
Si hemos puesto los rectángulos apaisados, las diagonales se aproximan a la recta de pendiente Φ. Si los hemos puesto verticales, se aproximan a la recta con pendiente 1/Φ

La espiral de Fibonacci
Una representació amb rectangles de la successió de Fibonacci ens va donant, en créixer, una aproximació cada cop més ajustada del rectangle auri.
En aquest mòdul els successius quadrats són peces de fusta, i, a partir dels dos quadrats inicials, es poden anar afegint quadrats fins a obtenir un rectangle molt pròxim al rectangle auri.
A més, en cada un d’aquests quadrats hi ha gravat un quart de cercle que, en fer la construcció dels rectangles, va construint una espiral, l’espiral de Fibonacci.


