The succession of Fibonacci. The number auri Φ

- Hotel Area: George Polya Room
- Minimum age: from 10 years old.
- Required time: 5 minutes.
- Number of participants: One or more people
- Keywords: art, philotaxis
- Taxonomy: GEOMETRY
Leonardo de Pisa (1170–1250) is known as Fibonacci. His commercial trips to North Africa motivated him to bring the hidu-Arabic numeracy system to Europe. In his Liber abaci we find the problem:
"A man put a pair of rabbits surrounded everywhere by a wall. How many rabbit couples can produce from that couple for a year if each couple is supposed to spawn a new partner every month and can only reproduce from the second month?"
This problem can be solved with this scheme where each circle means a pair of rabbits, in new pair blue and in red when it can be reproduced. Each column represents one month. The number of couples we have every month is the Succession of Fibonacci.
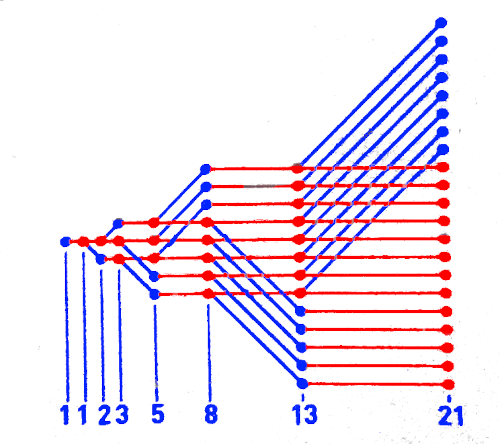
Fibonacci's succession is obtained recursively. It starts with a 1 in the first two terms, from there each term is obtained as the sum of the previous two
1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, 8+13=21, 13+21=34 ...
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, ...
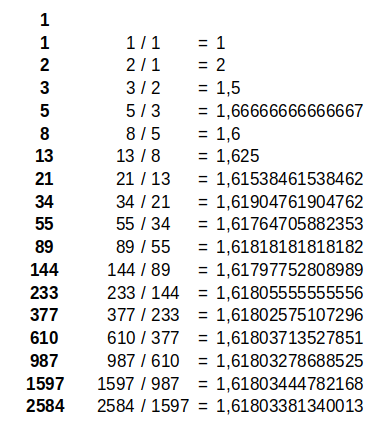
If to see the proportion of the growth in the number of rabbit pairs month by month, we divide those of one month by those of the previous month, we obtain different results, but they increasingly resemble and tend to the number of gold Φ. This is an irrational number whose expression in the decimal system has infinite numbers that are not repeated periodically.
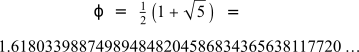
The Daisy
With this module you can experience how the number of gold present in nature.
The daisy is a composite flower. What in a simple flower would be petals, are in the daisy outer flowers that act as petals, are called lígulas.
The ligulas are not distributed symmetrically and even look messy. It may seem that they are distributed chaotically, but in fact the position where they are born is the most efficient so that they do not cover up with each other.
The module shows a daisy with numbered ligulas so that the number 1 is the furthest or oldest and the 13 is the closest or most recent. You can experience how by sliding the auri arch (from 137.5º) around the daisy goes from one ligula to the next.

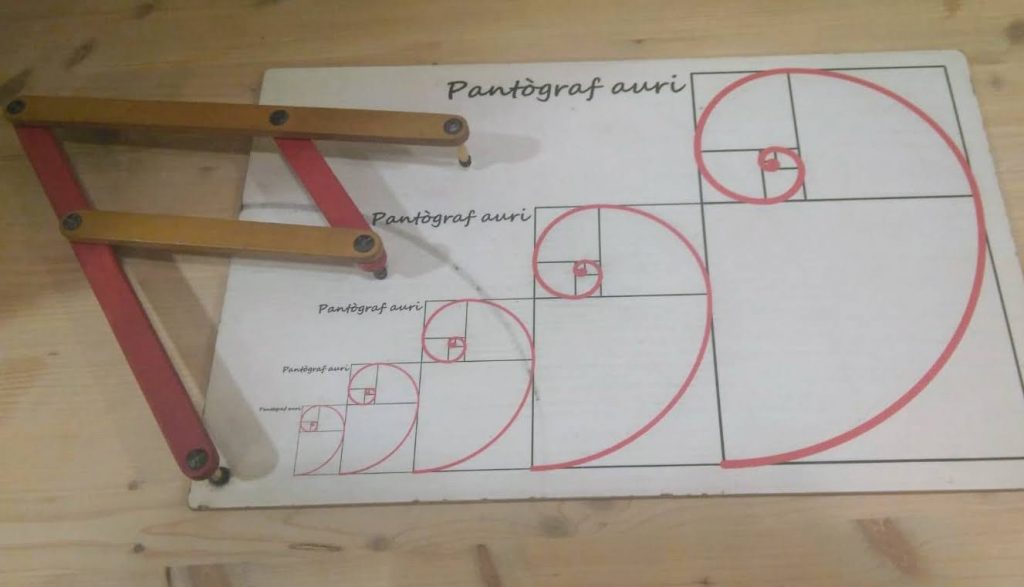
Golden pantograph
A pantograph is a drawing instrument used to copy scale drawings.
In real pantographs, the scale can be adjusted by changing the length of the arms and connection points. In this pantograph the scale is adjusted to 1:Φ , works like a golden compass.
In addition, the drawings are golden spirals, following with one arm a spiral, the other arm if I had a pencil attached, I would draw the other spiral.
Rectangles de Fibonacci
If we have the rectangles with sides the consecutive numbers of the Fibonacci succession so that they coincide with the lower vertex, we will see how its diagonal approaches one of the two straight lines drawn.
If we have put the rectangles off, the diagonals approach the slope Φ. If we have put them vertical, approach the straight with slope 1/Φ

Fibonacci's spiral
Una representació amb rectangles de la successió de Fibonacci ens va donant, en créixer, una aproximació cada cop més ajustada del rectangle auri.
En aquest mòdul els successius quadrats són peces de fusta, i, a partir dels dos quadrats inicials, es poden anar afegint quadrats fins a obtenir un rectangle molt pròxim al rectangle auri.
A més, en cada un d’aquests quadrats hi ha gravat un quart de cercle que, en fer la construcció dels rectangles, va construint una espiral, l’espiral de Fibonacci.


