La successió de Fibonacci. El nombre auri Φ

- Ubicació: Sala George Polya
- Edat mínima: a partir de 10 anys.
- Temps requerit: 5 minuts.
- Nombre de participants: Una o més persones
- Paraules clau: art, filotaxi
- Taxonomia: GEOMETRIA
Leonardo de Pisa (1170-1250) és conegut com a Fibonacci. Els seus viatges comercials al nord d’Àfrica el van motivar a portar a Europa el sistema de numeració hidu-aràbic. En el seu Liber abaci hi trobem el problema:
“Un home va posar una parella de conills envoltats per tots els llocs per una paret. Quantes parelles de conills es poden produir d’aquella parella durant un any si se suposa que cada mes cada parella engendra una nova parella i que només es poden reproduir des del segon mes?”
Aquest problema es pot resoldre amb aquest esquema on cada cercle significa una parella de conills, en blau parella nova i en vermell quan es pot reproduir. Cada columna representa un mes. El nombre de parelles que tenim cada mes és la successió de Fibonacci.
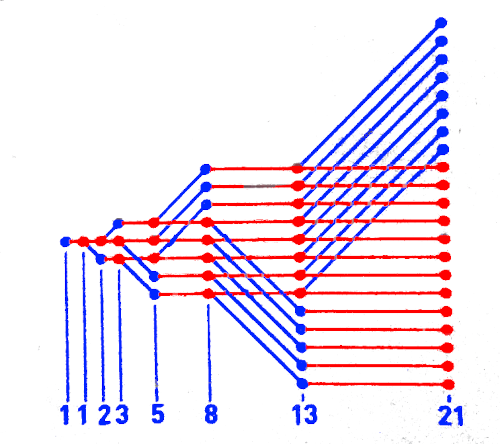
La successió de Fibonacci s’obté de manera recursiva. S’inicia amb un 1 als dos primers termes, a partir d’aquí cada terme s’obté com la suma dels dos anteriors
1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, 8+13=21, 13+21=34 …
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, ...
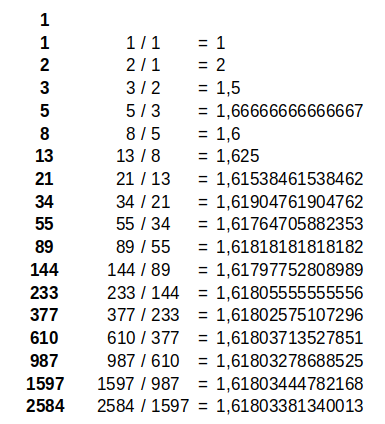
Si per veure la proporció del creixement del nombre de parelles de conills mes a mes, dividim les d’un mes per les del mes anterior, obtenim resultats diferents, però cada vegada s’assemblen més i tendeixen al nombre d’or Φ. Aquest és un nombre irracional l’expressió del qual en el sistema decimal té infinites xifres que no es repeteixen periòdicament.
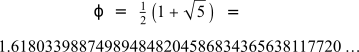
La margarida
Amb aquest mòdul es pot experimentar com el nombre d’or present a la naturalesa.
La margarida és una flor composta. El que en una flor simple serien els pètals, són en la margarida flors exteriors que fan de pètals, s’anomenen lígules.
Les lígules no estan repartides simètricament i fins i tot es veuen desordenades. Pot semblar que estan repartides caòticament, però de fet la posició on van naixent és la més eficient per tal que no es tapin unes amb les altres.
Al mòdul s’hi veu una margarida amb les lígules numerades de manera que la número 1 és la més allunyada o antiga i la 13 és la més propera o recent. Es pot experimentar com fent lliscar l’arc auri (de 137,5º) al voltant de la margarida es va d’una lígula a la següent.

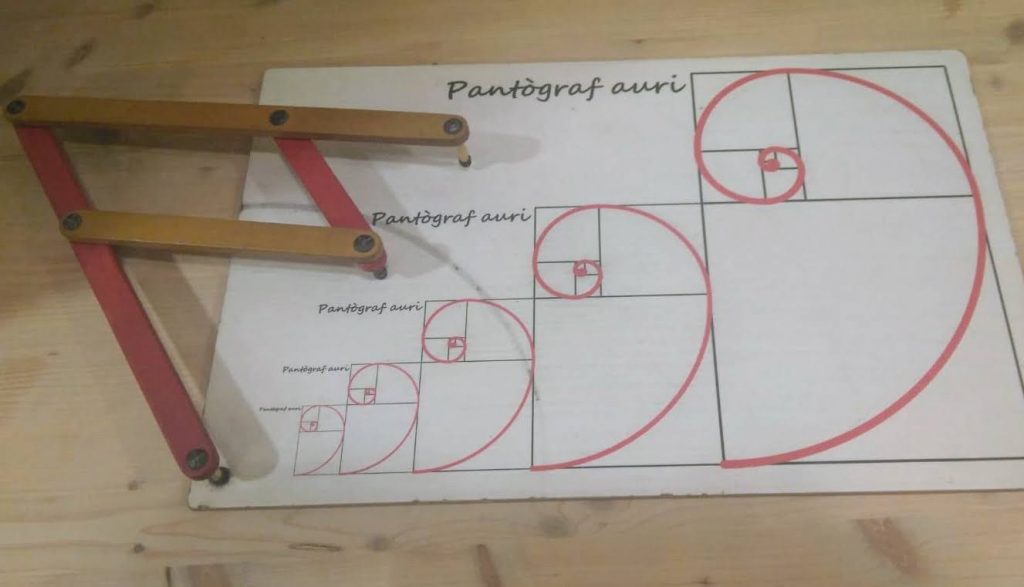
Pantògraf auri
Un pantògraf és un instrument de dibuix que serveix per a copiar dibuixos a escala.
En els pantògrafs reals, l’escala es pot ajustar canviant la longitud dels braços i els punts de connexió. En aquest pantògraf l’escala està ajustada a 1:Φ , funciona com un compàs auri.
A més a més els dibuixos són espirals àuries, resseguint amb un braç una espiral, l’altre braç si tingués un llapis enganxat, dibuixaria l’altra espiral.
Rectangles de Fibonacci
Si disposem els rectangles amb costats els nombres consecutius de la successió de Fibonacci de forma que coincideixin en el vèrtex inferior, veurem com la seva diagonal s’aproxima a una de les dues rectes dibuixades.
Si hem posat els rectangles apaïsats, les diagonals s’aproximen a la recta de pendent Φ. Si els hem posat verticals, s’aproximen a la recta amb pendent 1/Φ

L’espiral de Fibonacci
Una representació amb rectangles de la successió de Fibonacci ens va donant, en créixer, una aproximació cada cop més ajustada del rectangle auri.
En aquest mòdul els successius quadrats són peces de fusta, i, a partir dels dos quadrats inicials, es poden anar afegint quadrats fins a obtenir un rectangle molt pròxim al rectangle auri.
A més, en cada un d’aquests quadrats hi ha gravat un quart de cercle que, en fer la construcció dels rectangles, va construint una espiral, l’espiral de Fibonacci.


