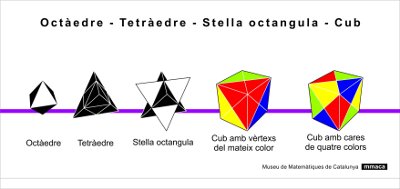
Sigue esta secuencia de construcción:
Parte del octaedro, es la pieza blanca y negra de 8 caras triangulares.
Enganchando los imanes los 4 tetraedros negros. El resultado un tetraedro negro de arista doble.
Engancha los 4 tetraedros blancos. El resultado es una estrella de 8 puntas (Stella octangula), formada por dos tetraedros intersecados.
Para acabar pone las piezas rojas, amarillas, verdes y azules para obtener un cubo.
¿Lo puedes hacer de forma que las piezas de un mismo color coincidan en un vértice?
¿Lo puedes hacer de forma que en cada cara del cubo haya los 4 colores?
- Ubicación: Sala Pere Puig Adam
- Edad mínima: a partir de 6 años.
- Tiempo requerido: 5 minutos.
- Número de participantes: Una o más personas
- Palabras clave: poliedros, tetraedro, octaedro, cubo, stella octangula.
- Taxonomía: Geometría





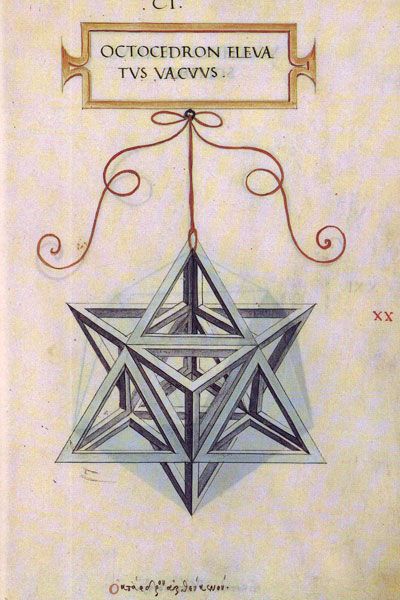
La estrella de 8 puntas o Stella octangula
Esta figura fue dibujada por Leonardo de Vinci como ilustración de la obra la Divina Proportione (1509) de Luca Pacioli, con el nombre de Octocedron Elevatus Vacuus.
Más adelante, Johannes Kepler en su libro De Nive Sexangula (1611). le dio el nombre de Stella Octangula
Como he podido comprobar a pesar de su aspecto punzocortado, sus vértices están situados exactamente en los vértices de un cubo.
Los volúmenes de los tetraedros, el octaedro y el cubo
- Todas las piezas tetraédricas de este módulo tienen el mismo volumen. Para justificarlo, comprueba que poniendo las piezas de color adecuadamente, todas tienen la misma base (un triángulo equilátero) y la misma altura (pone de lado un tetraedro de color y un negro). Llamamos a este volumen T.
- Comparemos el volumen del tetraedro negro de arista doble que se ha construido al principio con el volumen T de uno de los tetraedros regulares pequeños. Son figuras parecidas de razón 2. La razón de los volúmenes es 2³. Así pues, el tetraedro negro de arista doble tiene volumen 8T.
- Se puede calcular el volumen del octaedro del interior del tetraedro negro de arista restante de 8T los tetraedros que hemos pegado. ¿Cuál es pues el volumen del octaedro?
- Y también podemos calcular el volumen del cubo final en función de T contando cuántos tetraedros se han puesto sobre el octaedro. Recuentalos para comprobar que el cubo final tiene volumen 24T
Un altre possible enfoc sobre els càlculs dels volums
Módulos relacionados
- En el módulo Encajando poliedros de esta misma sala se puede ver un cubo con un tetraedro encajado dentro de él de la misma forma que lo están en este módulo.
- El módulo Longitud, superficie y volumen de esta sala muestra cómo hacen falta 8 esferas pequeñas para equilibrar una esfera del doble de diámetro. Es el mismo motivo por el que el tetraedro de arista doble que se ha montado en este módulo tiene volumen 8 veces el del tetraedro pequeño parecido.
