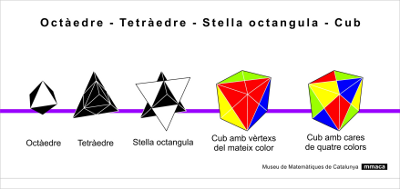
Follow this build sequence:
It starts from the octaheder, it is the white and black piece with 8 triangular faces.
Stick using the magnets on the 4 black tetraedras. The result is a double-edged black tetraedr.
Paste the 4 white tetraetrae. The result is an 8-pointed star (Stella octangula), made up of two intersecting tetraahedras.
Finally put the red, yellow, green and blue pieces to obtain a cube.
Can you do it in a way that the pieces of the same color match in a vertex?
Can you do it so that on each side of the cube there are 4 colors?
- Hotel Area: Sala Pere Puig Adam
- Minimum age: from 6 years old.
- Required time: 5 minutes.
- Number of participants: One or more people
- Keywords: polyhedras, tetrahedre, octahedr, cube, stella octangula.
- Taxonomy: Geometry





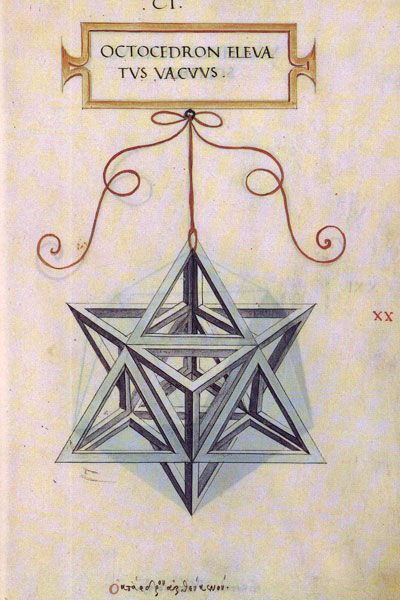
The 8-Pointed Star or Stella Octangula
This figure was drawn by Leonardo de Vinci as an illustration of Luca Pacioli's Divine Proportione (1509), under the name Octocedron Elevatus Vacuus.
Later, Johannes Kepler in his book De Nive Sexangula (1611). gave it the name Stella Octangula
As you could see despite its pointed appearance, its vertices are located exactly at the vertices of a cube.
The volumes of tetraetrae, octahedre and cube
- All the tetraendrial pieces in this module have the same volume. To justify this, check that by putting the colored pieces properly, they all have the same base (an equilateral triangle) and the same height (sideways a tetraheder of color and a black one). We call this volume T.
- We compare the volume of the double-edged black tetraeder that was built at first with volume T of one of the small regular tetraetraetraeres. They are similar figures of reason 2. The ratio of volumes is 2³. Thus, the double-edged black tetraeder has volume 8T.
- You can calculate the volume of the octaheder inside the remaining black tetraedr of 8T the tetraetraeres that we have attached to it. So what is the volume of the octaheder?
- And we can also calculate the volume of the final cube depending on T counting how many tetraahedres have been placed on the octahedre. Count them to check that the final cube has volume 24T
Un altre possible enfoc sobre els càlculs dels volums
Related Modules
- In the module Fitting polyheders in this same room you can see a cube with a tetraheder fitted inside it in the same way that they are in this module.
- The Length, Surface and Volume module of this room shows how 8 small spheres are needed to balance a sphere twice the diameter. It is the same reason why the double-edged tetraeder that has been mounted in this module has volume 8 times that of the similar small tetraedr.
