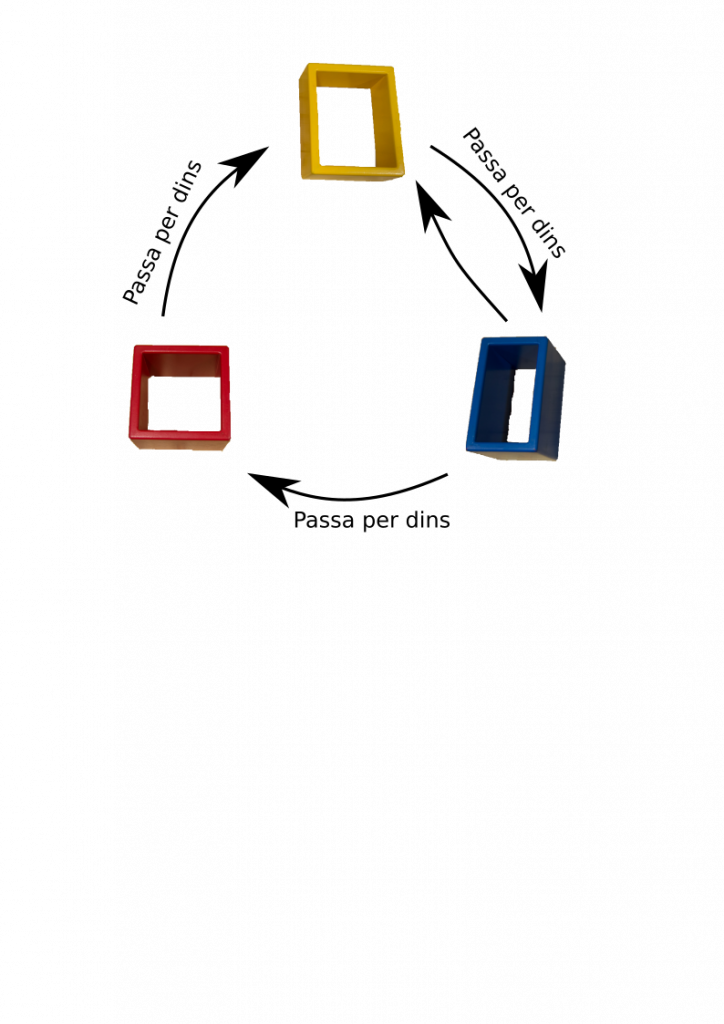Para ordenar estas 3 cajas, podemos utilizar muchos criterios, por ejemplo: altura, volumen, tamaño del agujero, tonalidad de color, etc.
Pero te proponemos investigar el criterio "PUEDE PASAR POR DENTRO"
Coge las cajas azul y roja, intenta pasar la roja por el agujero de la azul, ahora intenta pasar la azul por el agujero de la roja. Qué caja de las dos podemos considerar "pequeña".
Ahora confronta la azul con la amarilla. Cuál es la "pequeña" según este criterio.
Y para acabar compara la amarilla y la roja. ¿Cuál pasa por dentro?
En consecuencia, esta relación no establece una ordenación de ls 3 cajas.
- Ubicació: Actualment, fora de l'exposició
- Edad mínima: a partir de 6 años.
- Tiempo requerido: 5 minutos.
- Número de participantes: Una o más personas
- Palabras clave:
- Taxonomía:

Las relaciones no transitivas
Esta relación que hemos establecido entre cada dos cajas es circular. No es una relación de orden.
Otro ejemplo de estas relaciones es el juego "Piedra, papel, tijeras". El papel gana la piedra, las tijeras ganan el papel, pero las tijeras pierden frente a la piedra. No hay ganador absoluto.
Para que una relación entre elementos sea de ordenación es necesario que sea transitiva. Una relación es transitiva si siempre que el elemento A es más pequeño que el elemento B y B es más pequeño que C , entonces A es más pequeño que C. La relación "PUEDE PASAR POR DENTRO" entre estas cajas NO es transitiva.
El módulo "dados intransitivos" de la sala de estadística Lluís Santaló es otro ejemplo de este tipo de relación.