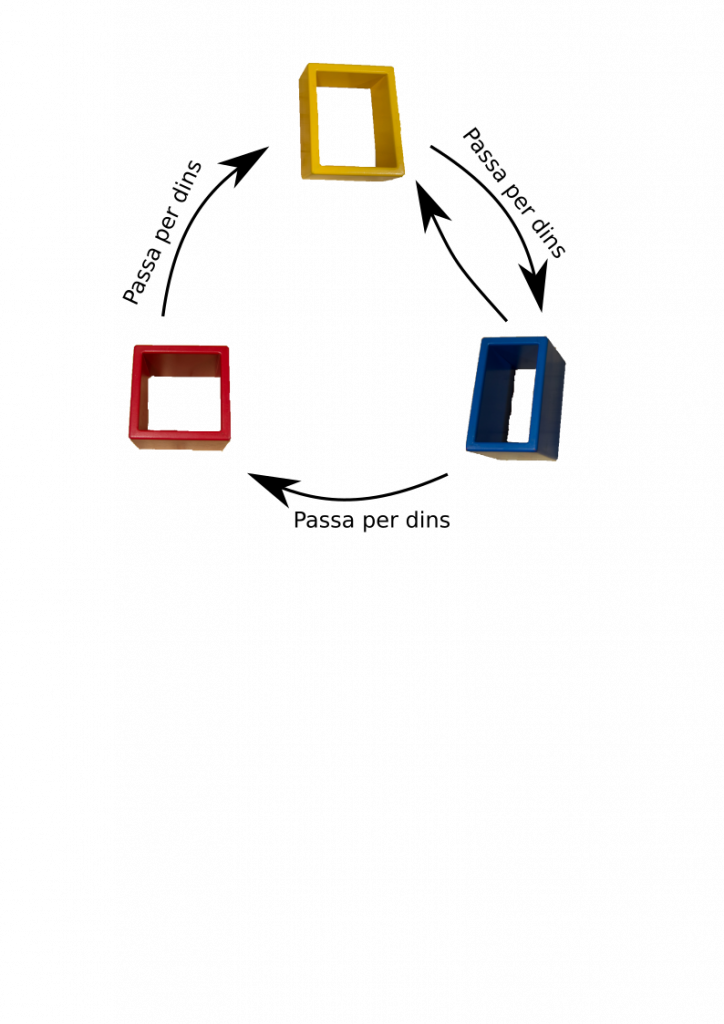To sort these 3 boxes, we can use many criteria, for example: height, volume, hole size, color shade, etc.
But we propose you to investigate the criterion "IT CAN PASS INSIDE"
He takes the blue and red boxes, tries to pass the red through the hole of the blue, now tries to pass the blue through the hole of the red. Which box of the two we can consider "small".
Now it confronts the blue with the yellow. What is the "small" according to this criterion.
And finally, compare yellow and red. What happens inside?
Consequently, this relationship does not establish an ordering of the 3 boxes.
- Ubicació: Actualment, fora de l'exposició
- Minimum age: from 6 years old.
- Required time: 5 minutes.
- Number of participants: One or more people
- Keywords:
- Taxonomy:

Non-transitive relationships
This relationship that we have established between each two boxes is circular. It is not a relationship of order.
Another example of such relationships is the game "Stone, paper, scissors." Paper wins the stone, scissors win the role, but the scissors lose to the stone. There is no absolute winner.
In order for a relationship between elements to be ordered, it must be transitive. A relation is transitive if whenever element A is smaller than element B and B is smaller than C , then A is smaller than C. The "CAN PASS INSIDE" relationship between these boxes is NOT transitive.
The "intransitive dice" module of the Lluís Santaló statistics room is another example of this type of relationship.