Posa les fitxes al tauler sense que es repeteixin ni els colors ni els valors ni a les files ni a les columnes.
Si ja l’has resolt, fixa’t com tens les diagonals, coincideixen valors o colors? Ara et proposem un segon repte: troba la solució canviant la configuració de les diagonals.
- Ubicación: Sala Martin Gardner
- Edad mínima: a partir de 6 años.
- Tiempo requerido: 5-10 minutos.
- Número de participantes: Una persona o más
- Palabras clave: Euler, problema de los 36 caballeros, sudoku
- Taxonomía: Historia de las matemáticas, Matemática computacional, 1


El cuadrado grecolatino 10×10 contraejemplo de la conjetura de Euler realizado manualmente en punto de cruz. ¿Cuántos puntos tiene?

Las soluciones del reto 4 filas, 4 columnas y 2 diagonales
Con la condición de que tampoco en las diagonales haya números o colores repetidos, hay 1.152 soluciones diferentes.
Una solución se puede transformar en otra permutando una característica. Por ejemplo si cambiamos todas las fichas de color verde por las de color azul con el mismo número o bien si cambiamos las fichas con el 2 por las del 4 con el mismo color. Como hay 4 variantes de cada característica, esto da 4!· 4! = 576 formas de transformar una solución en otra.
Las 1.152 soluciones son pues esencialmente solo dos soluciones, cada una con sus 576 variantes.
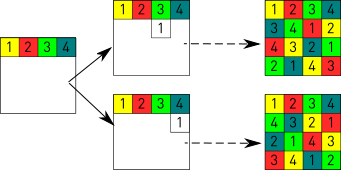
Si se llena la primera fila de la manera que muestra la imagen (habrían 576 formas diferentes de hacerlo) entonces en la segunda fila el 1 solo puede ir a la 3a o a la 4a columna. Fijada esta pieza, las restricciones ya condicionan y obligan a todas las demás colocaciones.
Historia de los cuadrados grecolatines
Estos cuadrados se llaman grecolatines porque históricamente las dos características que variaban, que aquí son las cifras y los colores, eran las letras del alfabeto latino y del alfabeto griego.
El matemático Leonhard Euler en 1780 estudió estos cuadrados por los diferentes tamaños del tablero y se dio cuenta de que no podía hacerlo por tableros de 6×6, escribió así el problema:
Se trata de hacer desfilar en filas y columnas a 36 oficiales de 6 rangos y 6 regimientos diferentes de forma que no haya rangos ni regimientos repetidos ni en filas ni en columnas.
Euler conjeturó que no existían soluciones para tableros NxN con N=6, 10, 14, 18, 22, ...
Hasta el año 1901 no se demostró que efectivamente no hay cuadrados grecolatines 6×6. La conjetura de Euler siguió abierta hasta el año 1959 cuando se descubrió un cuadrado grecolatino de 22×22 y poco después uno de 10×10. Además se demostró por cualquier N hay cuadrados grecolatines NxN excepto por N=2 y por N=6.
