Posa les fitxes al tauler sense que es repeteixin ni els colors ni els valors ni a les files ni a les columnes.
Si ja l’has resolt, fixa’t com tens les diagonals, coincideixen valors o colors? Ara et proposem un segon repte: troba la solució canviant la configuració de les diagonals.
- Ubicació: Sala Martin Gardner
- Edat mínima: a partir de 6 anys.
- Temps requerit: 5-10 minuts.
- Nombre de participants: Una persona o més
- Paraules clau: Euler, problema dels 36 cavallers, sudoku
- Taxonomia: Història de les matemàtiques, Matemàtica computacional, 1


El quadrat grecollatí 10×10 contraexemple de la conjectura d’Euler realitzat manualment en punt de creu. Quants punts té?

Les solucions del repte 4 files, 4 columnes i 2 diagonals
Amb la condició que tampoc a les diagonals hi hagi nombres o colors repetits, hi ha 1.152 solucions diferents.
Una solució es pot transformar en una altra permutant una característica. Per exemple si canviem totes les fitxes de color verd per les de color blau amb el mateix nombre o bé si canviem les fitxes amb el 2 per les del 4 amb el mateix color. Com que hi ha 4 variants de cada característica, això dona 4!·4! = 576 formes de transformar una solució en una altra.
Les 1.152 solucions són doncs essencialment sols dues solucions, cadascuna amb les seves 576 variants.
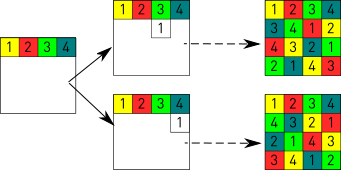
Si s’omple la primera fila de la manera que mostra la imatge (hi haurien 576 formes diferents de fer-ho) llavors a la segona fila l’1 sols pot anar a la 3a o a la 4a columna. Fixada aquesta peça, les restriccions ja condicionen i obliguen totes les altres col·locacions.
Història dels quadrats grecollatins
Aquests quadrats s’anomenen grecollatins perquè històricament les dues característiques que variaven, que aquí són les xifres i els colors, eren les lletres de l’alfabet llatí i de l’alfabet grec.
El matemàtic Leonhard Euler el 1780 va estudiar aquests quadrats per les diferents mides del tauler i es va adonar que no podia fer-ho per taulers de 6×6, va escriure així el problema:
Es tracta de fer desfilar en files i columnes a 36 oficials de 6 rangs i 6 regiments diferents de forma que no hi hagi rangs ni regiments repetits ni en files ni en columnes.
Euler va conjecturar que no existien solucions per taulers NxN amb N=6, 10, 14, 18, 22, …
Fins a l’any 1901 no es va demostrar que efectivament no hi ha quadrats grecollatins 6×6. La conjectura d’Euler va seguir oberta fins a l’any 1959 quan es va descobrir un quadrat grecollatí de 22×22 i poc després un de 10×10. A més es va demostrar per qualsevol N hi ha quadrats grecollatins NxN excepte per N=2 i per N=6.
