Posa les fitxes al tauler sense que es repeteixin ni els colors ni els valors ni a les files ni a les columnes.
Si ja l’has resolt, fixa’t com tens les diagonals, coincideixen valors o colors? Ara et proposem un segon repte: troba la solució canviant la configuració de les diagonals.
- Hotel Area: Sala Martin Gardner
- Minimum age: from 6 years old.
- Required time: 5-10 minutes.
- Number of participants: One person or more
- Keywords: Euler, problem of the 36 knights, sudoku
- Taxonomy: History of Mathematics, Computational Mathematics, 1


The Greco-Latin square 10×10 counterexample of the Euler conjecture made manually at cross point. How many points does it have?

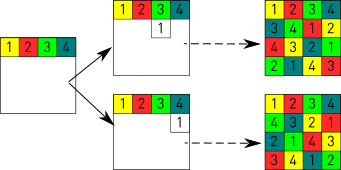
The solutions of the challenge 4 rows, 4 columns and 2 diagonals
Provided that there are also no repeated numbers or colors on the diagonals, there are 1,152 different solutions.
One solution can be transformed into another by permuting a feature. For example, if we change all the green tiles to the blue ones with the same number or if we change the tiles with the 2 to the 4 with the same color. Since there are 4 variants of each feature, this gives 4!· 4! = 576 ways to transform one solution into another.
The 1,152 solutions are essentially just two solutions, each with its 576 variants.
If the first row is filled in the way the image shows (there would be 576 different ways to do it) then in the second row the 1 can only go to the 3to or the 4to column. Once this piece has been fixed, the restrictions already condition and oblige all other placements.
History of Greco-Roman squares
These squares are called Greco-Roman because historically the two characteristics that varied, which here are the figures and colors, were the letters of the Latin alphabet and the Greek alphabet.
The mathematician Leonhard Euler in 1780 studied these squares for the different sizes of the board and realized that he could not do it for 6×6 boards, he wrote the problem thus:
It is about parading in rows and columns to 36 officers of 6 ranks and 6 different regiments so that there are no repeated ranks or regiments either in rows or columns.
Euler conjectured that there were no solutions for NxN boards with N=6, 10, 14, 18, 22, ...
Until 1901 it was not shown that there are indeed no Greco-Roman squares 6×6. Euler's conjecture remained open until 1959 when a Greco-Latin square of 22×22 was discovered and shortly afterwards a 10×10 square. It was also proved by any N there are Greco-Roman squares NxN except for N=2 and for N=6.
