En aquest aparell, hi ha dues pistes una recta i una altra en forma d’U molt oberta. Les dues pistes coincideixen en dos punts, el punt inicial a l’extrem superior i el punt final mitja altura de l’altre costat. Si des del punt més alt deixem anar a la vegada dues pilotes una per cada pista:
¿Qué vendrá antes del punto final? ¿Llegarán al mismo tiempo?





- Ubicación en el museo: Sala Pere Puig Adam
- Edad mínima: a partir de 4 años.
- Tiempo requerido: 5-10 minutos.
- Número de participantes: 1 o más.
Funcionamiento
Si lo has intentado, habrás observado que, claramente, la bola que hace la ruta curva llega mucho antes que la que hizo la ruta recta.
Esto puede ser sorprendente, ya que hemos aprendido que "la distancia más corta entre dos puntos es la línea recta". Hay que recordar que la pregunta inicial se refería al tiempo no a la distancia, la pelota que se encuentra con una pendiente más fuerte al principio coge más velocidad.
Hay, sin embargo, muchas maneras posibles de hacer esta curva: arco de circunferencia, parábola, elipse, etc. Precisamente, la de este dispositivo, es la forma en que se consigue la trayectoria más rápida. Se llama cicloide,es la trayectoria de un punto de una circunferencia al rodar sobre una línea recta. En el módulo, la cicloide está en una posición invertida con las puntas hacia abajo.
Contexto histórico
En el siglo XVII, el problema de la curva Tautocrónica (de los prefijos griegos tauto, que significa sí mismo y crono tiempo), era encontrar la curva donde un objeto toma lo mismo para llegar al punto más bajo independientemente del punto de partida. Christiaan Huygens en 1659 logró demostrar que la curva con esta propiedad es cicloide.
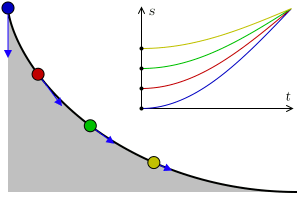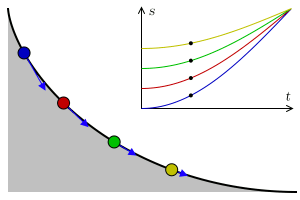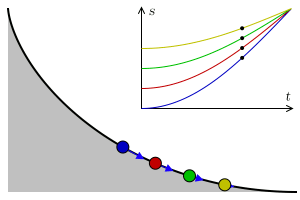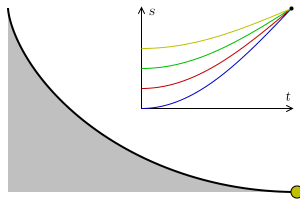
Puede consultar esta propiedad en el aparato del museo. Suelta al mismo tiempo dos bolas una a cada lado de la cicloide pero a diferentes alturas, verás que alcanzan el punto más bajo simultáneamente.
Johann Bernoulli en 1696 propuso a la comunidad matemática el problema de encontrar brachistochrone(del griego brachistos prefijos– que significa el tiempo más corto, y crono) es decir, la curva de descenso más rápida. Johann Bernoulli ya sabía que la solución es, de nuevo, cicloide. Las respuestas y trabajos de Leibniz, Newton, Jakob Bernoulli, Leibniz y Guillaume de Hôpital y Jakob Bernoulli sobre este problema condujeron al desarrollo de nuevas e importantes herramientas matemáticas. Es por eso que la cicloide ha sido nombradaHelena de la Geometría.
Material de extensión descargable
Gemma Ramírez ha realizado su Trabajo Fin de Grado en Matemáticas en la Universidad de Barcelona como proyecto de Aprendizaje y Servicio con el MMACA en esta curva.
En el artículo encontrarás un estudio de las propiedades geométricas y físicas de la cicloide, una revisión histórica de las contribuciones de los diferentes matemáticos así como un estudio con herramientas actuales.
Módulos relacionados
En este módulo las circunferencias de diferentes tamaños pueden rodar sobre otro fijo, los engranajes permiten hacerlo sin resbalar. Las curvas obtenidas son hipocicloides (si se enrollan en el interior) e hipocicloides (si se enrollan por fuera). Dependiendo de los tamaños relativos de la circunferencia fija y de la que rueda, se obtienen los diferentes tipos de estas curvas.
Las 5 piezas de madera de diferentes tonalidades con las que se construye este cono muestran los 4 tipos de secciones: Circunferencia, elipse, parábola e hipérbola.
La primera parte consiste en un engranaje de 50 dientes en cuyo interior se puede girar un círculo de 25 dientes, los 5 puntos de color del círculo siguen los 5 diámetros. La segunda parte es una pieza pentagonal con los 5 vértices de color situados en la misma posición que antes. El pentágono puede girar suavemente gracias a los cordones insertados en las trincheras construidas como los diámetros de la primera parte.



