En aquest aparell, hi ha dues pistes una recta i una altra en forma d’U molt oberta. Les dues pistes coincideixen en dos punts, el punt inicial a l’extrem superior i el punt final mitja altura de l’altre costat. Si des del punt més alt deixem anar a la vegada dues pilotes una per cada pista:
What will come before the end point? Will they arrive at the same time?





- Location in the museum: Sala Pere Puig Adam
- Minimum age: from 4 years old.
- Required time: 5-10 minutes.
- Number of participants: 1 or more.
functioning
If you have tried, you will have observed that, clearly, the ball that makes the curved route arrives much earlier than the one that made the straight route.
This can be surprising, since we have learned that "the shortest distance between two points is the straight line". It should be remembered that the initial question referred to time not distance, the ball that meets a stronger slope at the beginning picks up more speed.
There are, however, many possible ways to make this curve: circumference arch, parabola, ellipse, etc. Precisely, that of this device, is the way that achieves the fastest trajectory. It is called cycloid,it is the trajectory of a point of a circumference when rolling on a straight line. In the module, the cycloid is in an inverted position with the tips down.
Historical context
In the seventeenth century, the problem of the Tautochronic curve (of the Greek prefixes tauto, which means itself and chrono time), was to find the curve where an object takes the same to reach the lowest point independent of the starting point. Christiaan Huygens in 1659 managed to prove that the curve with this property is cycloid.
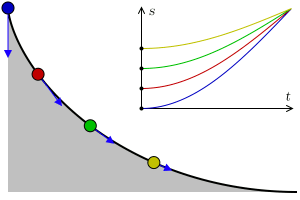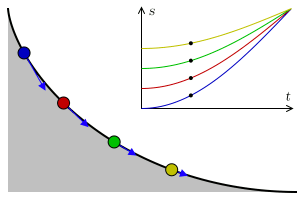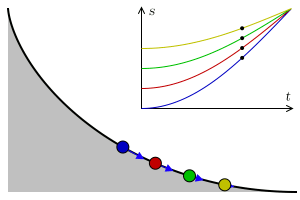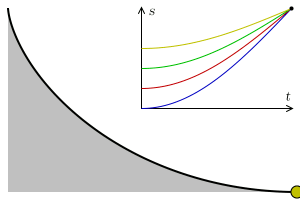
You can check this property on the museum's apparatus. Release at the same time two balls one on each side of the cycloid but at different heights, you will see that they reach the lowest point simultaneously.
Johann Bernoulli in 1696 proposed to the mathematical community the problem of finding brachistochrone(from the Greek brachistosprefixes – which means the shortest, and chrono time) that is, the fastest descent curve. Johann Bernoulli already knew that the solution is, again, cycloid. The responses and works of Leibniz, Newton, Jakob Bernoulli, Leibniz and Guillaume de Hôpital and Jakob Bernoulli on this problem led to the development of new and important mathematical tools. That is why the cycloid has been namedHelena of Geometry.
Downloadable extension material
Gemma Ramírez has done her Final Degree Project in Mathematics at the University of Barcelona as a Learning and Service project with the MMACA on this curve.
In the article you will find a study of the geometric and physical properties of cycloid, a historical review of the contributions of the different mathematicians as well as a study with current tools.
Related Modules
In this module the circumferences of different sizes can roll on another fixed, the gears allow to do it without slipping. The curves obtained are hypocycloids (if rolled inside) and hypocycloids (if rolled on the outside). Depending on the relative sizes of the fixed circumference and the one that rolls, the different types of these curves are obtained.
The 5 pieces of wood of different shades with which this cone is built show the 4 types of sections: Circumference, ellipse, parabola and hyperbola.
The first part consists of a gear of 50 teeth inside which can rotate a circle of 25 teeth, the 5 color points of the circle follow the 5 diameters. The second part is a pentagonal piece with the 5 color vertices located in the same position as before. The pentagon can rotate gently thanks to the laces inserted in the trenches built as the diameters of the first part.



