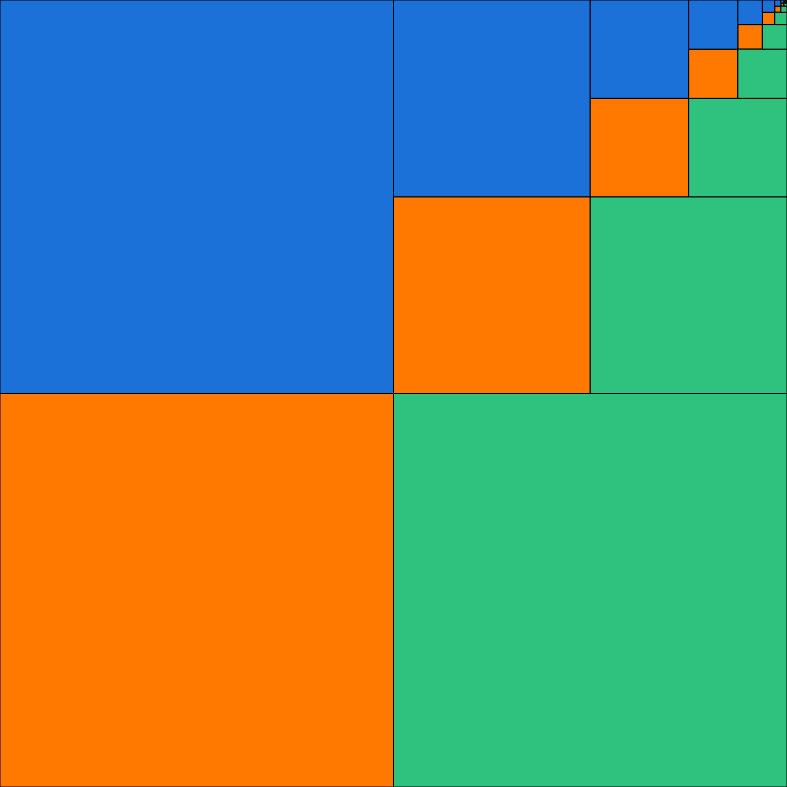
Observa aquest quadrat, està format per 3 sèries de quadrats marcats amb 3 colors diferents.
Cada sèrie comença per un quadrat de superfície 1/4 del quadrat general.
El segon terme és 1/4 de l’anterior, per tant, és 1/16 del total.
Segueix d’aquesta mateixa manera amb quadrats cada cop quatre vegades més petits.
És una suma d’infinits termes.
Com que les 3 sumes són iguals, cadascuna és 1/3 del quadrat general.
\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\frac{1}{256}+… =\frac{1}{3}
El full d'origami amb aquesta construcció
Podeu descarregar aquest full per fer aquesta atractiva demostració plegant un quadrat.
Convé imprimir-ho en una cartolina d’un color per cada cara.
Es retalla per tal que quedi el quadrat inicial i es fan els doblecs en muntanya i en vall segons indiquen les ratlles.
És una figura d’origami dissenyada per Jose Ignácio Royo Prieto.

- En venda a la botiga
- Edat mínima: a partir de 10 anys.
- Temps requerit: 5-10 minuts.
- Nombre de participants: Una o més persones
- Paraules clau: Sèrie, progressió, suma infinita, origami
- Taxonomia: Àlgebra
Una suma amb història
Aquesta suma ja es troba al llibre “La quadratura de la paràbola” d’Arquimedes de Siracusa (287 aC -212 aC).
La proposició 23 d’aquest llibre diu exactament:
Donades una sèrie d’àrees A,B,C,…,Z on A és la major i cadascuna és quatre vegades més petita que l’anterior, llavors:
A+B+C+D+…+Z+\frac{Z}{4}=\frac{4A}{3}
Fixeu-vos com, en aquesta formulació, s’esquiva parlar de suma d’infinits termes. El concepte d’infinit va ser acceptat pels matemàtics molts segles més tard.

