No és un cercle, però gira
Fes girar la peça dins el seu marc
Observa com sempre toca tots els costats del polígon.
Creus que funciona una bicicleta amb aquestes rodes?

- Edat: a partir de 6 anys.
- Temps mínim recomanat: 5 minuts.
- Paraules clau: Reuleaux, triangle, rotor, pi, amplada
- Geometria
El triangle de Reuleaux
Aquesta figura està formada per tres arcs iguals dibuixats amb centre els vertex d’un triangle equilàter i extrems els altres dos vèrtex.
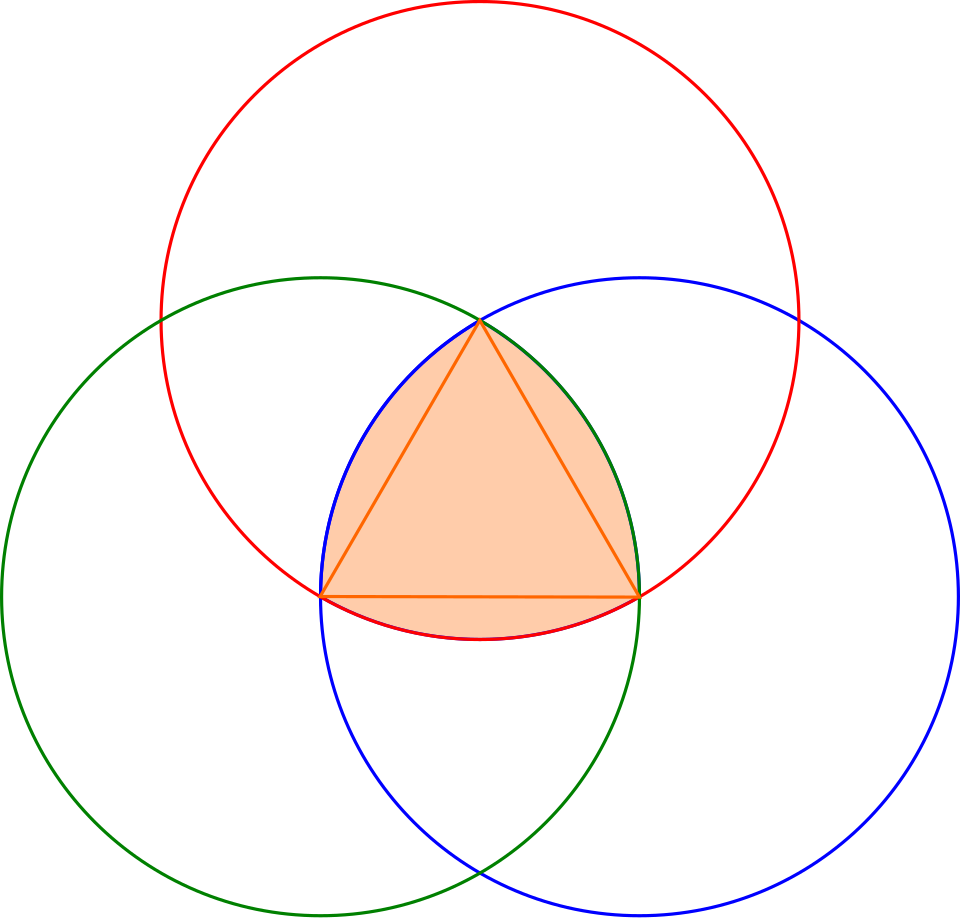
El cercle no és l'única figura amb la mateixa amplada en totes direccions.
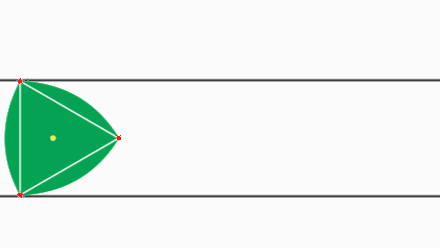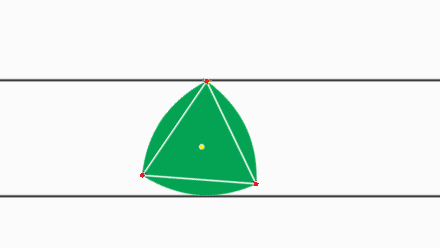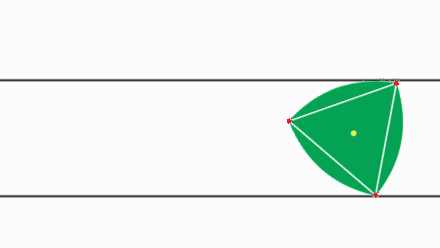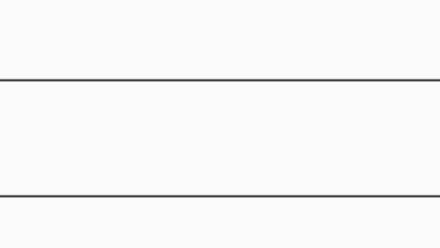
Tot i que intuïtivament si veiem una fusta rodant sobre uns cilindres mantenint l’alçada tendim a pensar que la secció dels cilindres un cercle, això no és necessàriament així.
El triangle de Reuleaux i moltes altres figures tenen la propietat que la seva amplada és constant.
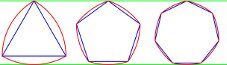
De la mateixa manera com s’ha fet el triangle de Reuleaux, es pot partir d’un pentàgon, heptàgon o un altre polígon regular amb un nombre senar de costats per construir figures d’amplada constant.
Més formes de construir figures d'amplada constant
Sorprenentment, les figures d’amplada constant poden ser irregulars.
Per exemple partint d’aquest pentàgon ABCDEF estrellat format per segments iguals i dibuixant els arcs corresponents, s’obté una figura d’amplada constant.
Mou A,B,C o D i crea la teva.
Un tercer mètode per dibuixar figures d’amplada constant:
Partint dels punts A,B i C, es dibuixen les rectes AB, AC i BC.
Llavors es dibuixa l’arc amb centre A delimitat per les rectes que passen per A.
S’enllaça aquest arc amb un altre de centre C.
Es continua enllaçant arcs fins a tancar la figura.
Mou A, B i C
I un altra construcció que es pot veure en aquest mòdul:
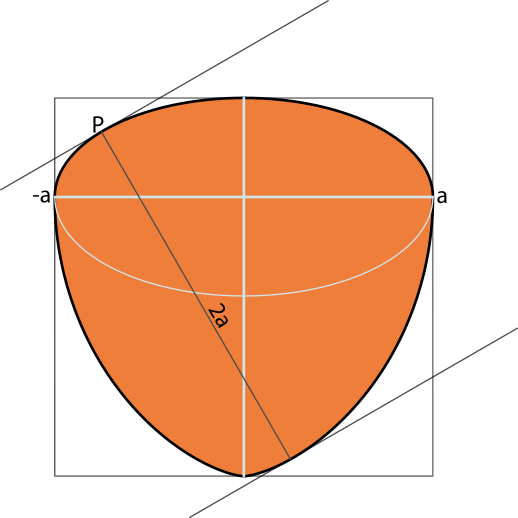
Parteix de mitja el·lipse: es pren la part de l’el·lipse que queda a una banda de l’eix major (-a.a) i es genera la part inferior com a lloc geomètric dels punts que estan a la distància 2a de cada punt P de la semiel·lipse en la direcció de la normal a aquest punt.
Funcionaria una bicicleta amb rodes triangles de Reuleaux?
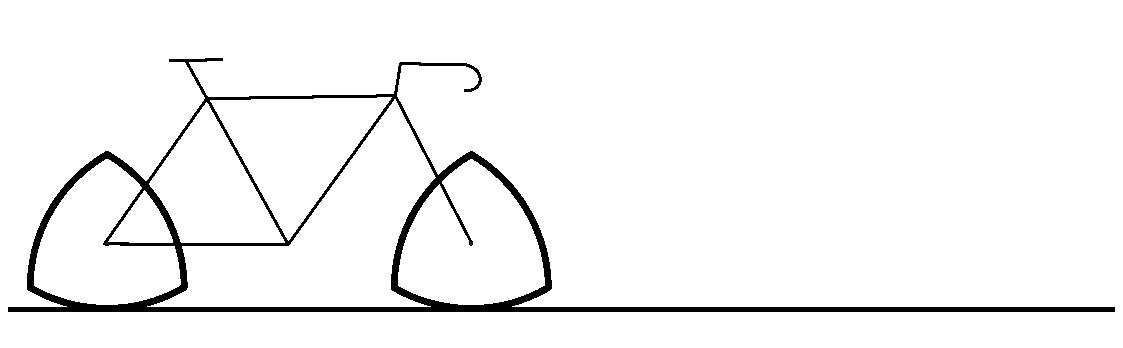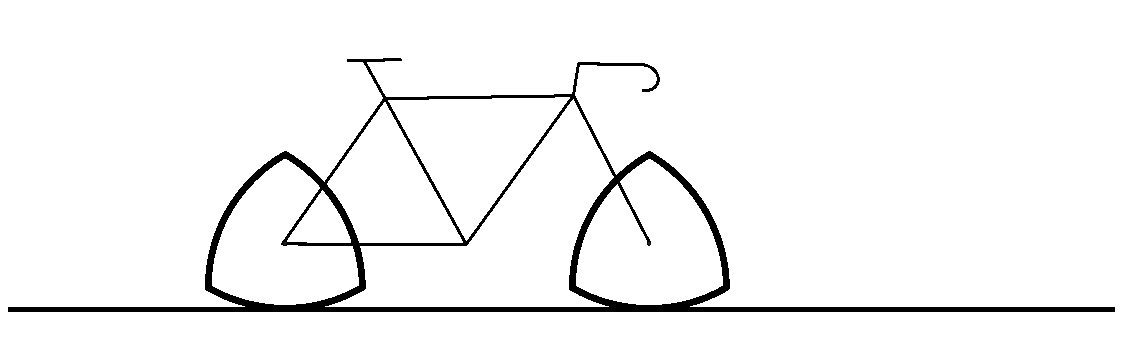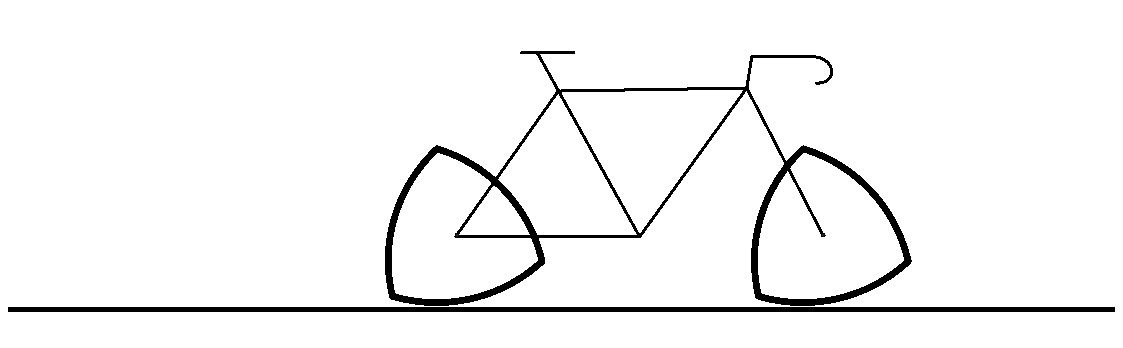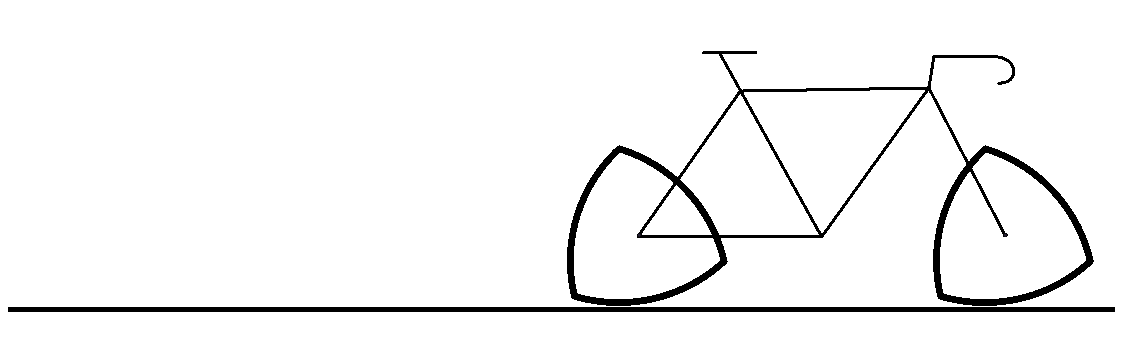
Tot i que el cercle i el triangle de Reuleaux mantenen la mateixa alçada, l’estructura de la bicicleta està subjecta a l’eix de la roda.
Com que el centre del triangle de Reuleaux puja i baixa, el ciclista es veurà sotmès a 3 sotracs per volta.
Perímetre del triangle de Reuleaux i de les figures d'amplada constant
Com mostra el vídeo, aquest mòdul permet comprovar que el perímetre del triangle de Reuleaux d’amplada constant 1 és π.
De fet, també tenen perímetre π totes les figures d’amplada constant. Aquest resultat es coneix com el Teorema de Barbier.
Podeu comprovar-ho amb les altres figures del mòdul.
Feynman i l'accident del transbordador espacial Challenger el 1986

El premi Nobel de Física Richard Feynman va ser un dels membres de la comissió encarregada d’esbrinar les causes d’aquest accident on el transbordador espacial Challenger es desintegrà 73 segons després d’enlairar-se.
Segons explica Feynman en el seu llibre “What Do You Care What Other People Think?” una de les raons que va trobar com a possible causa de l’accident era el mètode com els enginyers comprovaven que les juntes de les seccions del coet, que havien estat transportades horitzontalment, eren perfectament circulars.
El mètode era mesurar amb precisió els diàmetres cada 60º. Si les mesures dels 3 diàmetres coincidien consideraven que la secció era perfectament circular.
Això, evidentment no és suficient. Totes figures d’amplada constant passarien aquesta comprovació.
Aquest pot haver estat un dels factors de la fallada de les juntes de les seccions del coet que va causar el desastre.
Ús i aplicacions de les figures d'amplada constant.

El triangle de Reuleaux és una figura utilitzada sovint en l’arquitectura gòtica com veieu en aquesta imatge del claustre de la Catedral de Vic.

Les monedes de 50 penics del Regne Unit tenen el disseny d’un heptàgon de Reuleaux
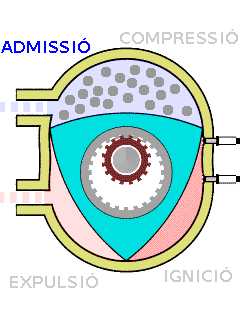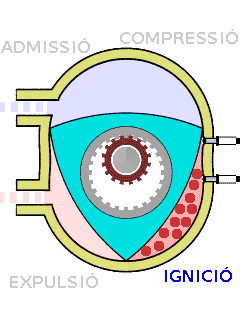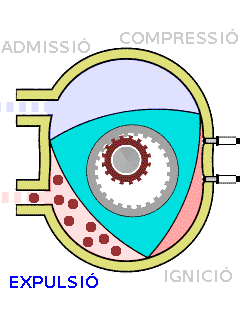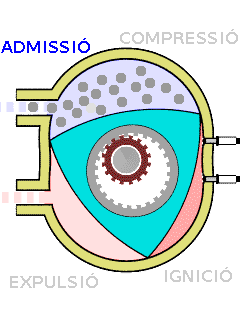
El motor Wankel és un motor de combustió interna rotatiu que en lloc dels pistons convencionals, fa servir un triangle de Reuleaux.
El premi del concurs videoMAT
El premi del concurs escolar de videoMAT, en funcionament des del curs 2012-2013, és un triangle de Reuleaux de fusta de pi realitzat pel nostre company Josep Rey.
En aquest vídeo es mostra com el perímetre del triangle de Reuleaux és π * amplada. De fet, això és una propietat de totes les figures d’amplada constant.
Enllaços externs
- Pàgina web amb molt bons vídeos o animacions https://etudes.ru/etudes/reuleaux-triangle/
- La pàgina de la Wikipèdia del Teorema de Barbier (totes les figures d’amplada constant a tenen perímetre π a )
- Article on s’expliquen els avenços actuals en la recerca de figures d’amplada constant en espais de dimensió superior https://www.quantamagazine.org
Escriu-nos
Si has trobat un error,
si creus que falta alguna cosa,
si vols aportar i compartir una activitat escolar relacionada amb aquest mòdul.
Escriu-nos !
