Frisos amb miralls paral·lels

Posa les 4 rajoles entre els dos miralls i mira el mosaic infinit que has creat.

  • Ubicació: Sala Emma Castelnouvo
  • Edat mínima: a partir de 6 anys.
  • Temps requerit: 5 minuts.
  • Nombre de participants: Una o més persones
  • Paraules clau: rajola de cartabó, rajola de mocadoret, reflexió, simetria, fris, mosaic
  • Taxonomia: Geometria, art

Les rajoles de cartabó o rajoles de mocadoret

Aquesta rajola bicolor formada per la divisió d’un quadrat en dos triangles per la seva diagonal és un dels dissenys tradicionals més antics que encara segueix vigent.

Ja és documentada al principi del segle XVII amb el nom de rajola mitadada. També és coneguda amb el nom de rajola de cartabó, rajola de vela o rajola de mocadoret.

La podem trobar per tot arreu, sota els balcons, en façanes, teulades, escales, bancs, paviments o parets. A vegades omplint l’espai ella sola, a vegades emmarcant figures o altres enrajolats.

Contrasta la seva senzillesa de disseny amb la versatilitat de dissenys que s’aconsegueixen combinant-les. Aquest un dels motius de la seva popularitat i importància patrimonial.

 

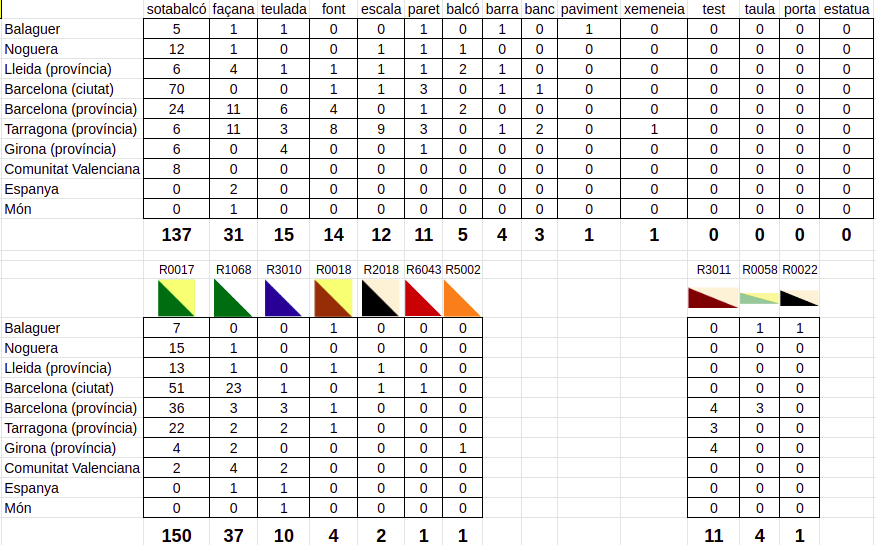
El company Ramon Tejedor (a twitter @Tejerauskas  a GeoGebra tejerauskas), ha fet una recopilació de localitzacions de la rajola cartabó a Catalunya.

El document conté les ubicacions d’aquests més de 330 indrets, la gran majoria en l’espai públic. Podeu col·laborar-hi enviant-li noves localitzacions.

Quants dissenys diferents hi ha amb aquestes 4 rajoles?

L’espai per a 4 rajoles que hi ha entre els dos miralls, es pot omplir ni més ni menys que de 256 formes diferents. Això és per què cada rajola es pot posar amb la fletxa que forma el triangle verd apuntant en 4 direccions, amb 4 rajoles tenim 4*4*4*4 = 256

Si considerem iguals els dissenys que coincideixen rodant el conjunt de les rajoles, cal dividir per 4 aquesta xifra. 

256/4 = 64

A la imatge es mostren 8 d’aquestes 64 formes diferents de posar 4 rajoles. A la dreta el fris(*) que es veu amb els miralls paral·lels. 

(*) Prenent el nom de fris com l’element arquitectònic en forma de banda horitzontal a les façanes dels edificis, en matemàtiques, un fris és un mosaic que s’estén en una sola direcció.

Es poden fer tots els frisos amb aquests dos miralls?

No, els miralls creen la repetició capgirant simètricament la imatge. Però al món físic real podem no capgirar les rajoles, simplement les podem traslladar i així construir mosaics sense simetria. Fixeu-vos en els frisos següents, no tenen cap simetria vertical.  Comprova com no es poden fer amb els 2 miralls paral·lels.

A diferència dels frisos de la imatge anterior, en què, si ens els imaginem dibuixats en una llarga tira de paper, la podem doblegar de forma que el fris d’un costat i l’altre coincideixin, en aquests frisos no hi ha forma en què doblegant la tira de paper coincideixin les figures.

Sebastien Truchet

Sebastien Truchet (Lió 1657–1729) va ser un polifacètic científic que va estudiar sistemàticament els múltiples patrons que es poden formar amb aquesta rajola. És per això que aquests mosaics són coneguts pels matemàtics i dissenyadors amb el nom de truchet tiling

Enllaços a materials