Vint-i-dos de juliol
Amb l’ajut de la cadena, comprova la relació aproximada que hi ha entre la longitud de la circumferència i el seu diàmetre.
Aquesta relació és constant i es coneix com a número pi
π soc irracional
- Edat mínima: a partir de 10 anys.
- Temps requerit: 5-10 minuts.
- Nombre de participants: Una o més persones.
- Paraules clau: pi, circumferència, diàmetre, irracional, aproximació
- Taxonomia: GEOMETRIA
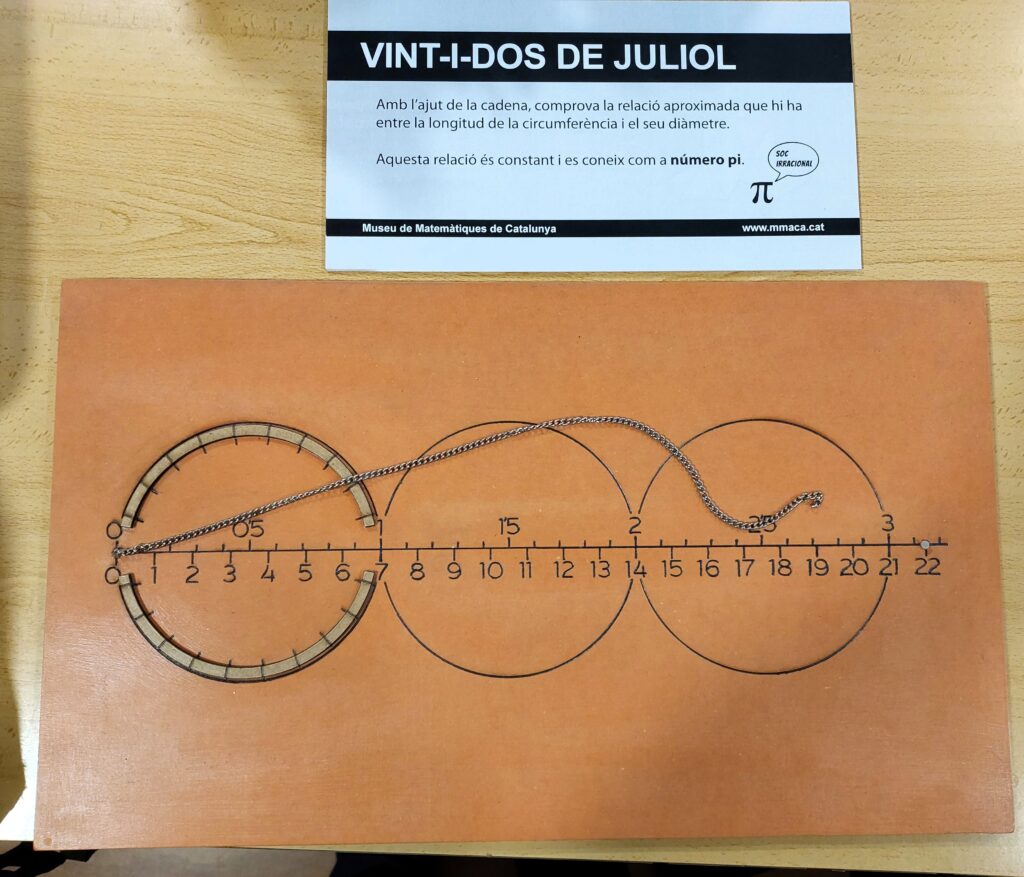
La cadena que hem posat al voltant de la circumferència la podem posar, a continuació sobre la línia horitzontal. Comprovem així que té la longitud de 3 diàmetres i “una mica més”.
Bona part de la història de les matemàtiques ha tingut com a objectiu la recerca del valor exacte d’aquest “una mica més de 3“
El 1761 J. H. Lambert va demostrar que aquest número, que anomenem amb la lletra grega π (pi), no es pot expressar com a fracció d’enters i que, per tant, la seva expressió decimal té infinites xifres decimals sense cap periodicitat. És el que anomenem nombre irracional.
L’aproximació més coneguda és 3,14
\Large \frac{longitud \; de \; la \; circumferència}{diàmetre}=\pi\simeq 3,14
I com que en el món anglosaxó s’anomenen els dies amb el mes davant, el dia 3-14 és el 14 de març. És el dia internacional de les matemàtiques.
I que el MMACA celebrem cada any.
Hi ha una altra aproximació de pi en forma de fracció
\Large \frac{longitud \; de \; la \; circumferència}{diàmetre}=\pi\simeq \frac{22}{7}
Seguint la mateixa lògica, el 22 de juliol es celebra el dia de l’aproximació de π
En aquest mòdul s’ha dividit el diàmetre en 7 parts. Es pot comprovar com la cadena s’estira 3 diàmetres i 1/7 més.
Escriu-nos
Si has trobat un error,
si creus que falta alguna cosa,
si vols aportar i compartir una activitat escolar relacionada amb aquest mòdul.
Escriu-nos!
