Conferència Online d'Adrián Paenza
Forzados a estar encerrados, tenemos la mente!
Dijous, 11 de juny del 2020 a les 19:00
Aquesta va ser la quarta de les sessions internacionals online aprofitant el confinament de la pandèmia.
Adrián Paenza és un matemàtic argentí, molt conegut arreu pels seus llibres d’enigmes i problemes de matemàtica recreativa, llibres que a més a més posa a disposició de tothom de forma lliure. A l’Argentina també és reconegut com a periodista de l’àmbit esportiu. Ha rebut múltiples premis com a divulgador científic.
Més informació del ponent
Los enigmas planteados por Adrián con algunas de las soluciones aportadas
Suponga que uno tiene 25 autitos, una pista para hacerlos dar vueltas. Solamente se permiten cinco autos por carrera. No hay cronómetro para determinar los tiempos.
Todo lo que se puede hacer al terminar una carrera, es ordenarlos por orden de llegada. ¿Se puede diseñar una estrategia de manera tal de poder seleccionar los tres más rápidos usando nada más que siete carreras (en total)?
Como se ve, el problema consiste en diseñar una estrategia para seleccionar los autitos para cada carrera. Esa es la parte que le corresponde a usted.
Yo ya lo “ayudé” cuando le dije que con siete carreras alcanza. Ahora se queda usted con la chance de pensar.
– Hacemos 5 grupos de 5. Cada grupo hace una carrera. Dentro de cada grupo los coches quedan ordenados así: A-B-C-D-E.
– Hacemos una carrera entre los 5 ganadores (los A) i ordenamos los grupos según haya quedado su coche A en esta sexta carrera:
Grupo cuyo A ha llegado 1º –> Los etiquetamos A1-B1-C1-D1-E1
Grupo cuyo A ha llegado 2º –> Los etiquetamos A2-B2-C2-D2-E2
Etc.
– Ya solo hay que tener en cuenta las 3 primeras “diagonales”:
A1 B1 C1
A2 B2
A3
porque con las relaciones de orden establecidas en la matriz descartamos así todos los coches que tienen por delante tres o más coches más rápidos que ellos.
Como ya sabemos que A1 es el más rápido, solo hay que hacer correr a los otros cinco la última carrera. Los dos que queden primeros serán el segundo y tercero más rápidos del total, respectivamente.
NOTA: en cambio a partir del que quede tercero en esta última carrera, no podremos garantizar que ocupen las posiciones absolutas de 4º, 5º, etc., puesto que hemos descartado coches que también podrían serlo.
(aportado por Carlos Luna)
Un río separa dos ciudades. Dos barcos lo recorren en direcciones opuestas a velocidad constante, no necesariamente la misma, pero mantienen la misma velocidad a lo largo del trayecto.
Más aún: cuando un barco llega del otro lado, da la vuelta inmediatamente sin detenerse y vuelve hacia el lugar de origen. Y repiten el proceso una y otra vez.
Los barcos salen al mismo tiempo. Se encuentran por primera vez en el camino a 7 kilómetros de una de las costas, y continúan su trayecto. Cuando cada uno llega del otro lado, como escribí más arriba, da la vuelta inmediatamente. Los barcos vuelven a encontrarse un a segunda vez, esta vez a 4 kilómetros de la costa opuesta.
¿cuál es el ancho del río?
Sea: x la amplitud del río, V i W las velocidades, T y T’ los tiempos de encuentro.
Para el primer encuentro tenemos dos ecuaciones:
7=V*T
x-7=W*T
de las que deducimos 7/(x-7) = V/W la razón de las velocidades
Para el segundo encuentro son:
x+4=V*T’
2x-4=W*T’
i por tanto (x+4)/(2x-4) =V/W
igualando y resolviendo x = 17km
(aportado por Enric Brasó)
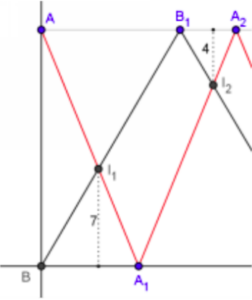Representando gráficamente la situación, a partir de la
semejanza de los triángulos de altura 7 y 4 tendremos
Si BA1 = m y AB1 = n
(2m – n)/4 = m/7 y por tanto 10m=7n
y si BA = k
(k-7)/n = 7/m
k – 7 =10
k=17
Se observa que las velocidades son proporcionales a 1/m y 1/n, por tanto estarán en proporción 10/7.
También tiene interés ver donde se sitúan los puntos de encuentro en 7 viajes del barco rápido (que corresponden a 10 del barco lento).
(aportado por Manel Udina)
Cuando los barcos se encuentran por primera vez, entre los dos han recorrido el ancho del río y el barco lento ha recorrido 7 km.
En el segundo punto de encuentro entre los dos han recorrido 3 veces el ancho del río y el barco lento habrá recorrido 3*7=21 km que son 4 más que el ancho del río.
Por tanto el ancho del río es 21-4 = 17 km.
Suponga que usted entra en un bar. En la barra hay 25 asientos puestos en una hilera o fila (como en cualquier bar). La curiosidad es que todos los clientes que llegan al bar son antisociales. ¿Qué quiero decir con esto? Cada vez que alguien viene al bar, mira cuáles de los 25 asientos están disponibles y sigue la siguiente regla (no escrita) pero que todos cumplen: si todos los asientos están vacíos, se sienta en cualquier parte, pero si hay alguno o algunos ocupados, se sienta dejando la máxima distancia posible con los otros clientes que ya están ocupando algunos asientos. En particular, esto dice que nadie se sienta “al lado de nadie”, en el sentido de que si alguien entra y advierte que para sentarse tendrá que tener algún vecino, entonces “pega media vuelta” y se va.
Algo más que transforma esta escena en algo bizarro: el barman, si él pudiera, trataría de que aun siguiendo la regla que se autoimpusieron, siempre haya la mayor cantidad de clientes posibles. Pregunta: si el barman pudiera elegir dónde sentar al primer cliente, ¿dónde le convendría pedirle que se siente de manera tal de alcanzar ese número máximo? Es decir, se trata de que usted elabore una estrategia de manera tal de que empezando con el bar totalmente vacío, en el momento en el que empiecen a llegar clientes, la decisión del barman permita llegar al máximo posible cumpliendo las reglas auto-impuestas.
Razonamiento “de atrás hacia adelante”:
La posición óptima es de 13 personas sentadas en los asientos impares 1,3,5,7,9,11,13,15,17,19,21,23,25
Solo se ocupara el asiento 3 si la persona encuentra ocupados los asientos 1 y 5. Solo se ocupará el asiento 5 si la persona encuentra ocupados asientos 1 i 9. Solo se ocupará el asiento 9 si se encuentran ocupado los asiento 1 i 17.
Hay que colocar la primera persona o bien en el asiento 9 o bien en el 17 que son posiciones simétricas.
Si llamamos “silla de oro” a la silla en la que colocamos la primera persona, nos planteamos:
¿Siempre, para cualquier número de sillas, existe la silla de oro?
En lugar de sillas pensamos en espacios, entre 25 sillas hay 24 espacios, los hemos dividido en dos grupos uno de 8 y otro de 16 espacios. Los espacios que son potencias de dos (2,4,8,16,32,…) son los que nos permiten dividirlos sucesivamente por la mitad y colocar las personas óptimamente
Para que exista la silla de oro el número de sillas ha de ser de la forma 2n+1 o bien 2n+2m+1.
3=2+1, 5=2²+1, 7=2²+2+1, 9=2³+1, 11=2+2³+1, 13=2²+2³+1, … , 25=2³+2⁴+1, …
15 es el menor entero que no es de esta forma. No existe silla de oro para una fila de 15 sillas. Se puede comprobar estudiando todas las posibilidades.
Con un número par de sillas, la colocación óptima permite un único tramo de 2 sillas libres contiguas, esto aumenta las posibilidades de “buenas colocaciones”. Pero la existencia de la silla de oro no se puede tampoco garantizar. Estudiando caso por caso he comprobado que no existe silla de oro para una fila de 30 sillas.
(aportado por Enric Brasó)
Usted pone en una urna 50 bolitas blancas (B) y 50 bolitas negras (N). El juego consiste en lo siguiente: usted mete la mano en la urna, y sin mirar, retira dos bolitas. Si las dos que sacó son del mismo color, repone una bolita negra. Si son de diferente color, repone la blanca. Y repite el proceso (suponga que usted tiene disponibles todas las bolitas que requiera para reponer segun estas reglas). Evidentemente, en cada paso hay una bolita menos dentro de la urna. Por lo tanto, habrá un instante en el que quedará una sola bolita. ¿De qué color será esa bolita?
Las bolitas blancas siempre se reducen en dos, ya que solamente se reduce su número si elegimos 2 bolitas blancas y se substituye por una negra. Es decir, siempre el número de bolitas blancas será PAR. Así, puesto que al inicio tenemos 50 bolas blancas, su número ira disminuyendo a 48, 46, 44, … 6, 4, 2, 0. La última bola será negra.
Es un ejemplo más de problema de paridad.
Organitza:
