Quina és la proporció de boles de color?
En aquest bombo transparent hi ha boletes de dos colors. Un llistó amb ranura permet recollir una mostra de 50 boletes. La proporció de boles de colors observada a la mostra, és una estimació de la proporció que ens demanen.
Fent lliscar una peça per tal que indiqui la proporció de la mostra, podem llegir l’interval de confiança del 95%, és a dir entre quins valors està la proporció de boles de color de tot el bombo.
- Ubicació en el museu: Sala Lluís Santaló
- Edat mínima: a partir de 12 anys.
- Temps requerit: 5-10 minuts.
- Nombre de participants: 1 o més si li cal ajuda per fer els càlculs.



Funcionament general
Cal fer girar el bombo de manera que el llistó de fusta quedi totalment ple, d’aquesta forma s’han seleccionat exactament 50 boletes.
Les 50 boletes del llistó són la nostra mostra aleatòria. Cal comptar quantes boletes blaves hi ha. Si, per exemple, contem 8 boletes blaves del total de 50, això vol dir que el percentatge de boletes blaves a la mostra és del 16%. Aquest és un càlcul mental fàcil de fer.
Un cop tenim el percentatge de la mostra o proporció mostral, hem moure a la peça de fusta adjunta al bombo, el seu lliscador fins que indiqui aquest valor. Llavors podrem llegir els valors mínim i màxim que ens indica per una mostra de mida 50. Aquest és l’interval de confiança on se situa, amb una probabilitat de 95%, el percentatge real de boletes de color.
Reflexionem: El resultat és realment un interval molt gran. Per poder ajustar més el resultat i obtenir un interval de confiança més petit hem de treballar amb una mostra més gran. Això ho podem fer amb el mateix bombo. Fem recollides de 50 boles i sumem els resultats. A la peça lliscant hi ha indicat l’interval de confiança per a mostres de diferent mida.
Conceptes relacionats
Context històric
A l’any 1937 ja es troben publicacions que desenvolupen el concepte d’interval de confiança. Tanmateix, es va trigar força temps a utilitzar-se de forma precisa i rutinària. Per exemple, no va ser fins al 1997 que un assaig amb un conjunt molt gran de mostres i un interval de confiança acceptable va poder assegurar que la teràpia amb cortisol no redueix el risc d’ictus aguts [font].
Comentaris
Extreure conclusions sobre unes dades a partir sols d’unes quantes mostres és un procés al què estem acostumats. Cal però ser conscients que requereix que la característica que estudiem estigui repartida de forma uniforme a tota la població i que ens assegurem que a l’agafar la mostra tots els elements tenen la mateixa probabilitat de ser triats.
Com anècdota, il·lustrativa: en el procés de construcció d’aquest mòdul vàrem haver de descartar una determinada remesa de boletes de colors doncs presentaven una lleugera adherència a les parets del bombo.
Aplicacions
A partir de les proporcions mostrals resulta relativament senzill aproximar les proporcions que es donaran a tota la població sense necessitat de mostrejar la població sencera. Això és molt útil a l’hora de trobar la prevalença (proporció) de determinades malalties en un país o fins o tot a nivell mundial. D’aquesta manera es pot trobar, per exemple, la proporció de fumadors d’un país i fer una previsió de la despesa sanitària que representaran en un futur.
Reproducció fàcil d'aquest mòdul a l'aula
Ens cal una caixa de metacrilat o altre material transparent i boletes de dos colors d’exactament la mateixa mida i característiques. Poden ser perles per fer collarets o polseres o bé, com les d’aquest mòdul, projectils per escopetes d’aire comprimit.
Cal omplir la caixa aproximadament fins a la meitat. i precintar-la amb cinta adhesiva per tal que no s’obri al remenar-la.
Un cop l’hàgim agitat podem considerar que la mostra és la fila de boletes que han quedat situades al llarg d’una de les arestes inferiors.
Simulació amb un full de càlcul
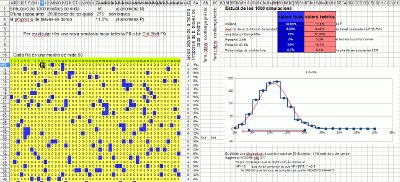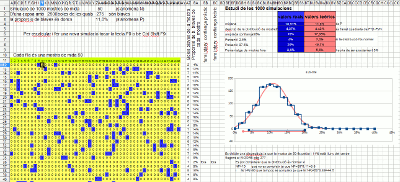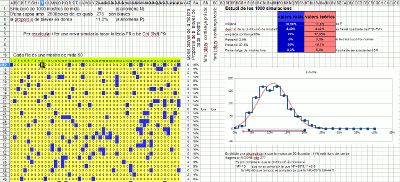
Els full de càlcul disposen de la funció que genera un nombre aleatori entre 0 i 1, normalment la seva sintaxi és =RAND(). També disposen d’una opció (normalment és F9) que recalcula tot el full i per tant renova tots aquests valors. Amb això es fonamenta aquest full de càlcul (XLS, ODS) on es simulen 1.000 extraccions d’una mostra de mida 50. D’aquestes 1.000 proporcions mostrals se’n fa un histograma (en blau) que es sobreposa amb la corba normal corresponent (en vermell). Es comprova que s’ajusta correctament i per tant es justifica l’amplada de l’interval de confiança utilitzat en el lliscador.
