Aprofita les simetries dels poliedres per veure’ls a traves dels miralls.
Posa les peces horitzontalment, sostingudes a banda i banda.
Comença per les peces que són una sola barra.
Totes les peces tenen una posició determinada en que encaixen amb els miralls. Busca-la
Quin poliedre veus? Localitza’l al cartell.
Treu les peces abans de posar-ne una altra
Quins angles formen els miralls?
Les tres taules que formen aquest mòdul tenen els 4 miralls disposats de forma que els angles entre ells (angles dièdrics) produeixen que els objectes es visualitzin 3, 4 o 5 cops.
- El primer calidoscopi té els 4 angles diedres entre els miralls de 120º. Com que cada angle triplica els objectes l’anomenem 3-3-3-3. Amb aquesta disposició un simple objecte allargat col·locat a l’interior es visualitza com un tetraedre regular.
- Els diedres del segon calidoscopi són de 120º, 90º, 120º i 90º. L’anomenem 3-4-3-4. Permet visualitzar el cub i l’octaedre regular.
- En el tercer calidoscopi els angles són 120º, 72º, 120º i 72º L’anomenem 3-5-3-5. Permet visualitzar l’icosaedre i el dodecaedre regulars.
A més a més, a cada calidoscopi, un conjunt de peces especials permeten obtenir els diferents truncaments. S’aconsegueixen veure més de 25 poliedres diferents.
- Ubicació: Sala Emma Castelnuovo
- Edat mínima: a partir de 10 anys.
- Temps requerit: 5-10 minuts.
- Nombre de participants: Una o més persones
- Paraules clau: simetries, calidoscopis, miralls, poliedres.
- Taxonomia: GEOMETRIA































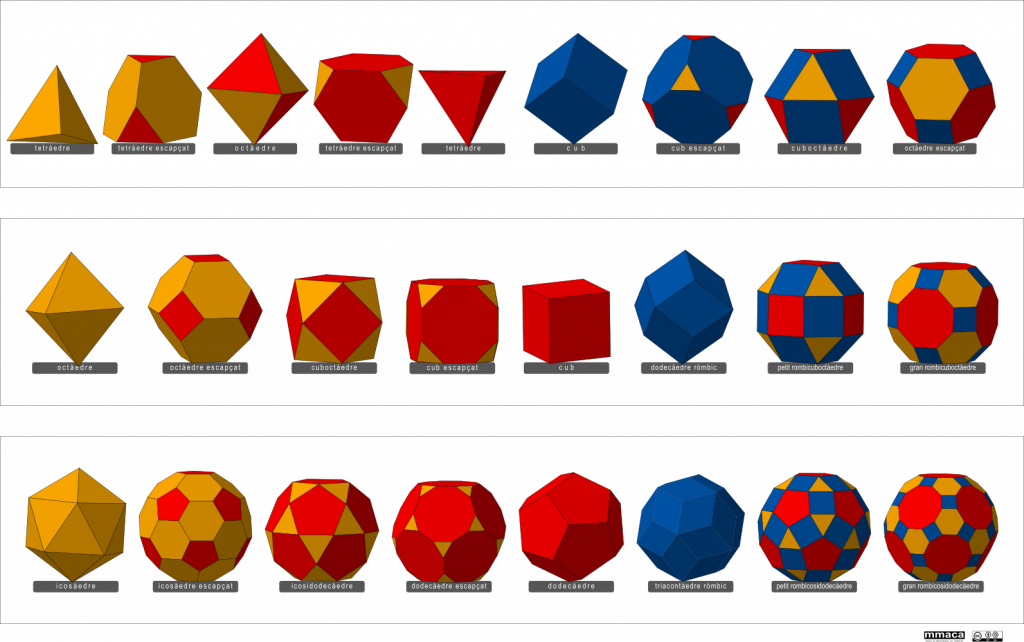
Els principals poliedres que es poden visualitzar amb els calidoscopis 3-3-3-3, 3-4-3-4 i 3-5-3-5
Enllaços externs i material descarregable
- Cartell amb els poliedres que es poden visualitzar a les taules de calidoscopis.
- Article de Josep Rey i Manel Udina a la revista NouBiaix sobre els calidoscopis i poliedres
- Apunts per treballar els mòduls d'aquesta sala preparats per l'Toni Gomà i Daniel Bosch
- Pàgina "Polyhedral_kaleidoscopes" de la mathcom.wiki
