Observa els colors de les cares dels daus, de les 6 cares n’hi ha dues vermelles, imagina que el vermell representa un verí.
Tirant un sol dau, què és més probable que surti verí o que no?
I tirant els dos daus? Què és més probable enverinar-se o no enverinar-se?
Per enverinar-se n’hi ha prou que un dels daus surti vermell!
Estudi experimental
Pots fer servir l’àbac com a comptador per descobrir aquestes probabilitats de forma empírica
- En el cas d’un dau, les probabilitats dels dos casos difereixen un 33%, així que ràpidament comprovaràs que és més probable no enverinar-se.
- En el cas dels dos daus, les dues probabilitats sols difereixen un 11%, així que potser hauràs de llençar-los més vegades per comprovar que és més probable enverinar-se.
Anàlisi de casos equiprobables
Podem suposar els daus regulars i equilibrats, llavors com que tenen sis cares , la probabilitat que quedin d’una cara determinada és 1/6 o del 16´6%
Amb un dau, les probabilitats són 2/6 o el 33’3% d’enverinar-se i 4/6 o el 66´7% de no enverinar-se.
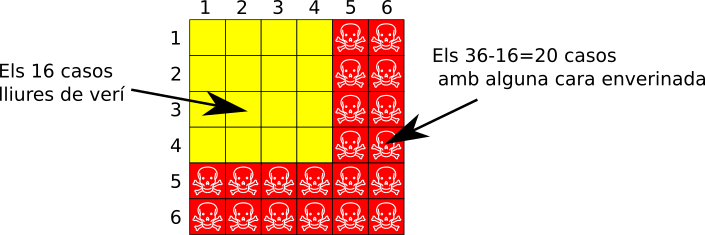
Amb dos daus cal distingir cara per cara els dos daus, hi ha 6 x 6 = 36 casos diferents equiprobables. Per calcular quants d’aquests casos tenen verí, és més senzill comptar el contrari: hi ha 4 cares sense verí d’un dau i 4 sense verí de l’altre dau combinant-les surten 4×4=16 casos sense verí. Tots els altres casos tenen o bé una cara amb verí o bé les dues, són 36-16=20 casos. Així que les probabilitats són 16/36 o 44´4% de no enverinar-se i 20/36 o el 56% d’enverinar-se.
- Ubicació: Sala Lluís Santaló
- Edat mínima: a partir de 10 anys.
- Temps requerit: 5 minuts.
- Nombre de participants: Una o més persones
- Paraules clau: Atzar, freqüència probabilitat.
- Taxonomia: Probabilitat i estadística
