Amb les mateixes peces reconstrueix els dos polígons.
En aquesta taula veuràs diferents trencaclosques. L’objectiu és, amb cada conjunt de peces, formar els dos polígons dibuixats.
- Ubicació: Sala Puig Adam
- Edat mínima: a partir de 6 anys.
- Temps requerit: 5-10 minuts.
- Nombre de participants: Una o més persones
- Paraules clau: geometria, trencaclosques
- Taxonomia: GEOMETRIA


El trencaclosques del mercader de roba de Dudeney
Al llibre “The Canterbury Puzzles, and Other Curious Problems” de del 1907, el matemàtic Henry Ernest Dudeney proposa el següent problema:
Es tracta de tallar una peça de roba en forma de triangle equilàter en quatre trossos per fer-ne un quadrat.
La solució és particularment interessant, ja que les peces es poden articular per formar els dos polígons com mostra l’animació.

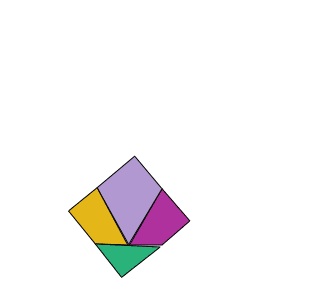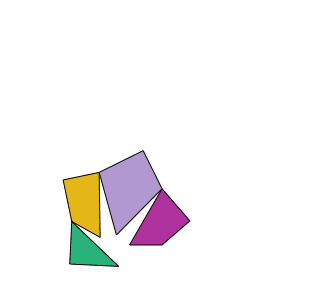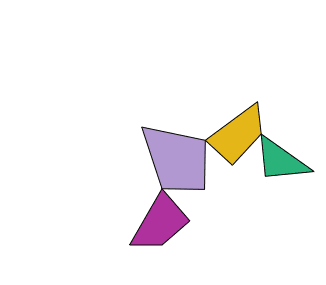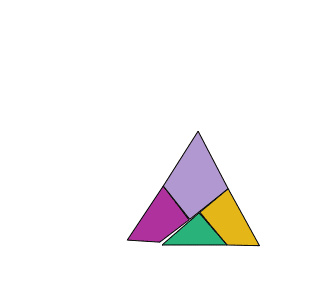
El cas general
El trencaclosques de transformar un triangle en quadrat i els altres d’aquesta taula són casos particulars d’un resultat matemàtic més general:
Donats dos polígons qualssevol de la mateixa àrea, sempre existeix una dissecció en un nombre finit de peces que permet, reorganitzant-les, formar cadascun dels dos polígons.
És el teorema de Wallace–Bolyai–Gerwien, anomenat així per què va ser demostrat, de forma independent, per aquests tres matemàtics.
El teorema diu que la dissecció existeix, però no diu pas com fer-la ni en quantes peces cal tallar. La forma de fer-ho, és diferent en cada cas. Sovint s’ha descobert més d’una forma de fer-ho, tanmateix, les més interessants són les que utilitzen menys peces. Aquesta pàgina recull les disseccions amb menys peces conegudes.
El fet que, sempre existeixi, una dissecció per a qualsevol parella de polígons amb la mateixa àrea, pot semblar una cosa molt òbvia, però sorprenentment, la qüestió anàloga a dimensió tres té una resposta negativa. Donats dos poliedres amb el mateix volum, no sempre és possible fer una dissecció en peces d’un poliedre que permetin reconstruir l’altre.
Les disseccions de la botiga del MMACA
A la botiga del MMACA trobareu aquestes diferents disseccions fabricades per nosaltres.
Altres mòduls
En aquest mòdul les circumferències de diferent mida poden rodar sobre una altra fixada, els engranatges permeten fer-ho sense que rellisquin. Els corbes que s’obtenen són les hipocicloides (si es fan rodar per l’interior) i les hipocicloides (si es fan rodar per l’exterior). En funció de les mides relatives de la circumferència fixa i la que roda s’obtenen els diferents tipus d’aquestes corbes.
Les 5 peces de fusta de diferents tonalitats amb què està construït aquest con mostren els 4 tipus de seccions: Circumferència, el·lipse, paràbola i hipèrbola.
La primera part consisteix en un engranatge de 50 dents a l’interior del qual pot girar un cercle de 25 dents, els 5 punts de color del cercle segueixen els 5 diàmetres. La segona part és una peça pentagonal amb els 5 vèrtexs de color situats a la mateixa posició que abans. El pentàgon pot girar suaument gràcies als encaixos inserits a les rases construïdes com els diàmetres de la primera part.




