Aquest polígon pot enrajolar tot el pla,
però només de forma no periòdica.
El març de 2023 va fer-se públic l’article que ho demostra.
- Ubicació en el museu: Sala Martin Gardner
- Edat mínima: a partir de 6 anys.
- Temps requerit: 5-10 minuts.
- Nombre de participants: 1 o més.
Quin és el "Problema d'Einstein"?
Es coneix amb aquest nom el problema, que consisteix a trobar una única tessel·la que enrajoli el pla de forma no periòdica.
El nom d’Einstein no té res a veure amb el conegut físic. Només és un joc de paraules en alemany, ja que ein Stein significa “una pedra” en aquest idioma.
Què és una tessel·lació no periòdica?
La majoria dels enrajolats o tessel·lacions del pla que veiem són periòdics, això significa que pots traslladar una còpia de l’enrajolat sencer fins a fer-la coincidir un altre cop amb ell mateix.
Els barrets d’Einstein poden recobrir tot el pla, però cap enrajolat format per ells serà periòdic. Les tessel·lacions amb aquesta propietat s’anomenen “no periòdiques”.
Aquests barrets d'Einstein resolen el "problema d'Einstein"?
Tot i que l’article on s’han donat a conèixer no ha estat revisat formalment per la comunitat matemàtica, tot sembla indicar que és correcte.
Queda pendent, però, trobar una tessel·lació aperiòdica formada per còpies d’una mateixa peça en la mateixa orientació.
En els enrajolats amb barrets d’Einstein la majoria de les peces estan orientades de la mateixa manera, però de tant en tant no queda més remei que fer servir la peça simètrica (amb orientació inversa).
En les peces del MMACA, les peces simètriques respecte a la majoria són les de color gris.
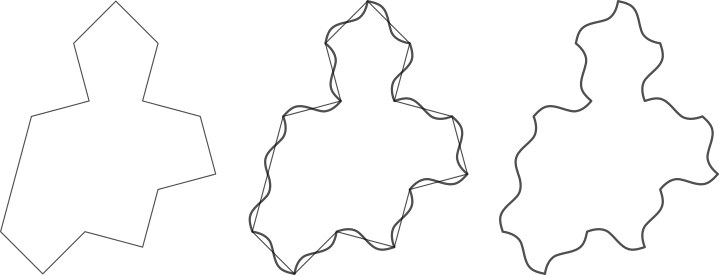
Quina és la forma exacta dels barrets d'Einstein?
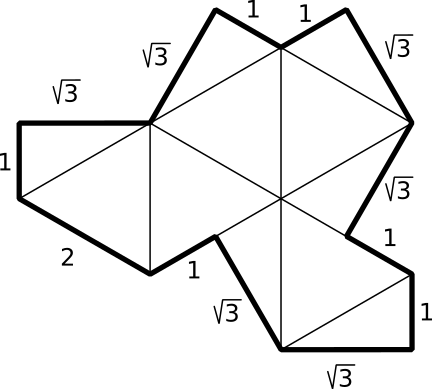
És un polígon còncau de 13 costats format la unió de 5 triangles equilàters i 6 meitats de triangles equilàters.
Els nusos dibuixats en la versió exposada al MMACA són una forma senzilla de distingir els costats de valor √3. Aquesta decoració és opcional, si es giren totes les peces, es pot fer servir la cara llisa.
Quina és la història del seu descobriment?
Aquesta forma va ser descoberta el novembre del 2022 per David Smith, un jubilat no matemàtic del nord d’Anglaterra. Sospitant que podria ser la solució del problema d’Einstein va contactar amb els matemàtics Joseph Samuel Myers, Craig S. Kaplan i Chaim Goodman-Strauss.
Amb l’estudi d’aquesta forma aquests matemàtics han descobert que forma part d’una família infinita de polígons que enrajolen el pla de forma no periòdica. L’article que han escrit presentant les seves investigacions conjuntament amb David Smith encara està pendent de revisió.
- L'article presentant aquesta rajola no periòdica (PDF 89 pag.)
- Gravació de la videoconferència entre els descobridors, la comunitat gathering4gardner.org i Roger Penrose
- Aplicació que permet crear diferents figures dins aquestes siluetes (barrets, samarretes, tortugues, ...)
- Model STL per imprimir en una impressora 3D
Animació extreta de https://youtu.be/W-ECvtIA-5A del canal de Craig S. Kaplan, que mostra de forma contínua la família de polígons d’aquesta descoberta que enrajolen el pla de forma no periòdica.