La lemniscata
La corba que simbolitza l’infinit

Quina és la definició de lemniscata?
La lemniscata és una corba descrita per Johann Bernouilli el 1694.
Es defineix com el lloc geomètric dels punts que el producte de les distàncies a dos focus és constant.
Prenent com a focus F’=(-a,0) i F=(a,0)
tindríem: distància AF * distància AF= a²
\sqrt{(x+a)^{2}+y^{2}}*\sqrt{(x-a)^{2}+y^{2}}=a^{2}
elevant al quadrat [(x+a)^{2}+y^{2}]*[(x-a)^{2}+y^{2}]=a^{4}
i seguint simplificant obtenim l’equació de la lemniscata
(x^{2}+y^{2})^{2} = 2a^{2}(x^{2}- y^{2})
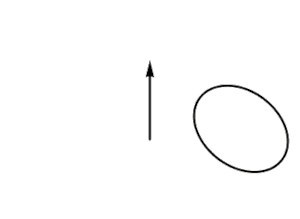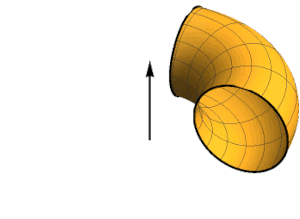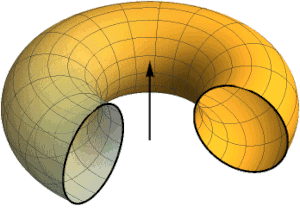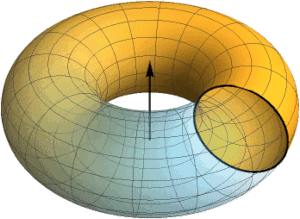
La lemniscata és la secció d’un tor particular
En geometria un tor és la superfície de l’espai que genera un cercle en girar al voltant d’un eix situat en el seu mateix pla.
De forma col·loquial és conegut també amb el nom d’un producte de pastisseria industrial.
En el cas que el radi interior del tor sigui igual al radi de la circumferència que el genera, llavors, en tallar el tor per un pla tangent al seu anell interior s’obté la lemniscata.


El mecanisme de Watt per dibuixar la lemniscata
James Watt (1736-1819), un enginyer escocès, treballant en el disseny pioner de la màquina de vapor, va idear un mecanisme que permetia convertir un moviment circular amb un moviment pràcticament rectilini.
En la construcció de GeoGebra, es pot veure el seu funcionament. Consta de 3 barres lligades pels seus extrems a dos punts fixats A i B . Les corbes que descriuen les trajectòries del punt mitjà de la barra central M reben el nom de corbes de Watt. Variant les longituds de les barres podeu obtenir-ne unes quantes.
En el cas AC=BD i CD= \sqrt{2} AC per exemple amb AC=BD=1 i CD=1.41 s’obté la lemniscata.
Amb els valors AC=BD=2 i CD=0.3 comprovareu com la corba és a la pràctica un segment recte.

Construcció adaptada a partir de la de Rafael Losada
El símbol de l’infinit
El matemàtic John Wallis en la seva obra “De sectionibus conici” del 1655 va proposar aquest símbol per el concepte d’infinit.
Es pot consultar aquesta obra la web archive.org
Desconeixem en què es va inspirar John Wallis per proposar aquest símbol ja que és anterior a la definició de Bernoulli i també al descobriment de la banda de Moebius

