L’inversor
Un aparell que transforma el moviment rectilini en moviment circular.
Mou el punt amb el pom de subjecció resseguint les rectes o circumferències dibuixades, comprova com el punt articulat de l’interior de l’estructura, segueix les circumferències o rectes del mateix color.

Què és la inversió geomètrica?
La inversió és una forma d’assignar a cada punt del pla un altre punt del pla de la següent forma:
Cal fixar d’entrada un punt O, centre de la inversió, que és invariant (es transforma en ell mateix) i un nombre positiu constant k (potència de la inversió). Llavors la imatge d’un punt P és el punt Q de la semirecta que passa per O i P que compleix que el producte de les seves distàncies al punt O és igual a k2
OP * OQ = k2
Mou el punt P, veuràs que està lligat a la circumferència vermella que passa per O.
El punt Q (imatge de P per la inversió) deixa un rastre. Quin?
Mou el centre de la circumferència vermella. Quin és ara el rastre de Q?
Torna a carregar la pàgina per esborrar el rastre.

La hipèrbola i la lemniscata són corbes inverses
En aquesta versió del mòdul es pot comprovar com resseguint la hipèrbola vermella, el punt interior de l’inversor ressegueix la corba en forma del símbol infinit anomenada lemniscata.
Quines propietats té la inversió?
Els punts de la circumferència de radi k amb centre O són punts invariants.
En la inversió tots els punts interiors a la circumferència fixa es transformen en punts exteriors i viceversa.
La inversió conserva els angles.
Les circumferències que passen per l’origen es transformen en rectes, les rectes que passen per l’origen es transformen en elles mateixes i les circumferències que no passen per l’origen es transformen en altres circumferències. En particular les circumferències que tallen perpendicularment la circumferència de punts fixos de la inversió es transformen en elles mateixes.
Podem dir que la inversió és com una simetria en què “el mirall” és la circumferència invariant.
Què és l’inversor de Peaucellier
Aquest mecanisme format amb barres articulades permet associar un punt amb el seu invers (amb les limitacions òbvies de l’objecte).
Fou inventat el 1864 pel francès Charles-Nicolas Peaucellier i va ser important en el desenvolupament de la màquina de vapor.
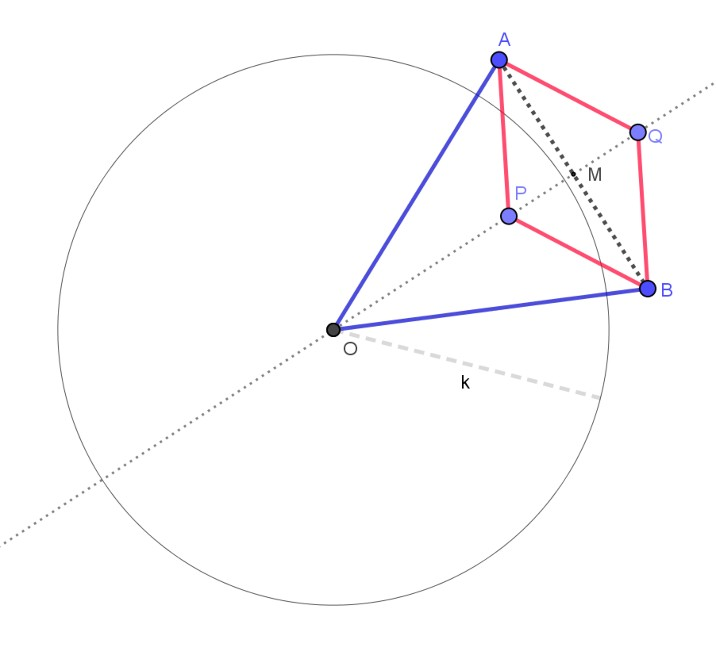
Consta de 4 barres iguals, en vermell en el dibuix AP = AQ = BP = BQ
i dues que les uneixen també iguals OA = OB
Quina és la justificació geomètrica de l’inversor?
Per veure que OP·OQ és constant cal jugar amb els triangles rectangles OMA i PMA i aplicar-hi el teorema de Pitàgores.
(OP+PM) 2+AM 2 = OA 2
PM 2+AM 2=AP 2
OQ=OP+2PM
OP 2+2OP·PM+PM 2+AM 2=OA2
OP(OP+2PM)+PM2+AM2=OA2
OP·OQ = OA2-AP2 que és constant i igual a k2