Col·loca les 16 fitxes en el marc quadrat 4×4 de manera que els colors dels costats que es toquen coincideixin.
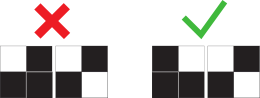
- Ubicació:
- Edat mínima: a partir de 6 anys.
- Temps requerit: 15 minuts.
- Nombre de participants: Una o més persones
- Paraules clau: Trencaclosques, simetria, quadrat
- Taxonomia: Geometria, Combinatòria
Més reptes? Ajuda?
Si ja ho has resolt, ara pots intentar més reptes:
- Col·loca les 16 peces amb les vores interiors coincidents i a més a més amb els colors de la vora de dalt coincidint amb els de la vora de baix. (seria una solució cilíndrica)
- I encara una tercera condició: Fes que, a més, els colors de la vora de la dreta coincideixen amb els de la vora esquerra. (solució “toroidal”)
És difícil?
Una ajuda:
Hi ha solucions simètriques (respecte a una diagonal), això a la vegada que t’imposa més condicions t’ajuda a trobar-les, ja que hi ha peces desaparellades que obligadament estan situades sobre l’eix de simetria.

Les 16 peces
Per construir les peces es divideix el quadrat en 4 quadrats iguals i es pinten de negre o blanc de totes les formes possibles diferents. No es tenen en compte les rotacions que farien algunes peces iguals.
Les solucions
Hi ha moltes solucions possibles, així que aconseguir-ne alguna és assequible.
Normalment, el procés és anar omplint el marc amb les peces fins que es detecta que cap de les peces que resten es pot posar, llavors és el moment de reflexionar i recol·locar alguna peça.
Us animem a compartir la vostra solució a les xarxes socials amb l’etiqueta #pandasquare

Ivan Moscovich, el gran iniciador dels museus científics interactius
Aquest trencaclosques apareix amb el nom de BITS en el llibre d’ Ivan Moscovich “Super games”. Una versió competitiva va ser comercialitzada amb el nom de Q-bit (⇒)
Ivan Moscovich va néixer de pares jueus a Vojvodina (actual Sèrbia) el 1926. A 17 anys va ser internat al camp de concentració d’Auschwitz. Va passar per 4 camps de concentració i 2 camps de treball forçat.
Acabada la guerra va estudiar enginyeria mecànica a la Universitat de Belgrad i va emigrar a Israel on va treballar com a investigador científic implicat en el disseny de materials didàctics, ajuts educatius i jocs educatius.
El 1964 va fundar el Museu de Ciència i Tecnologia de Tel-Aviv. Aquest va ser un dels museus que va canviar la forma expositiva tradicional, incorporant molts materials interactius de ciències, matemàtiques i art. Un dels seus visitants va ser el físic Frank Oppenheimer, les idees, dissenys i materials que hi va recollir van ser la llavor del revolucionari Exploratorium de San Francisco que Oppenheimer va inaugurar el 1969 i que encara ara és un referent dels museus interactius com el nostre.

Moscovich és un escriptor incansable, té més de 30 llibres a la web d’Amazon, tots ells recomanables que constitueixen una font inesgotable d’idees originals.
És també un gran creador de jocs com el mític “Magic robot”, “Magic mirror”, “Tricky fingers”, “30cubed” o “Fold”





Investigacions al voltant de les solucions
David Butler professor del Centre d’Aprenentatge de Matemàtiques de la universitat d’Adelaida (Austràlia) explica al seu blog com el 2016 va treure la idea del llibre d’Ivan Moscovich i li va posar el nom de PANDA SQUARE.
És interessant l’enumeració de les preguntes que planteja, algunes amb resposta, altres que encara resten obertes:
- És possible alguna solució amb algun tipus de simetria o rotació? Quines simetries es poden descartar?
- Quantes solucions hi ha?
- A partir d’una solució, quantes solucions derivades es poden trobar fàcilment?
- És possible tenir una solució on totes les rajoles idèntiques estiguin en una orientació diferent?
- Existeix una solució amb una sola regió negra connectada?
- Sembla que a les solucions trobades sempre almenys una de les rajoles totalment negres o totalment blanques estan a les vores. Es pot provar?
- És possible que la rajola totalment negra estigui a una vora i a la vora oposada hi hagi la rajola totalment blanca?

El 2020, David Butler va fer un fil explicant la troballa i demostració de les úniques 4 solucions simètriques.
A person Will Gibson emailed me out of the blue to tell me that he had found a Panda Squares solution that was symmetrical, even though back in 2016 I was pretty sure there weren't any that were symmetrical. VERY exciting! https://t.co/2El6FGrt4o pic.twitter.com/tlqzkR4gjo
— David Butler (@DavidKButlerUoA) February 2, 2020
So there are EXACTLY FOUR Panda Squares solutions with line symmetry (up to rotation). pic.twitter.com/AG0WHPX6jD
— David Butler (@DavidKButlerUoA) February 3, 2020
Associant cada peça amb la seva expressió en binari
Si identifiquem el color negre amb l’1 i el blanc amb el 0 i decidim un ordre pels 4 quadrats de cada peça que pot ser per exemple: superior-esquerra, superior-dret, inferior-esquerra, inferior-dret, llavors podem associar de forma unívoca cada peça amb l’expressió binaria dels nombres naturals del 0 al 15.
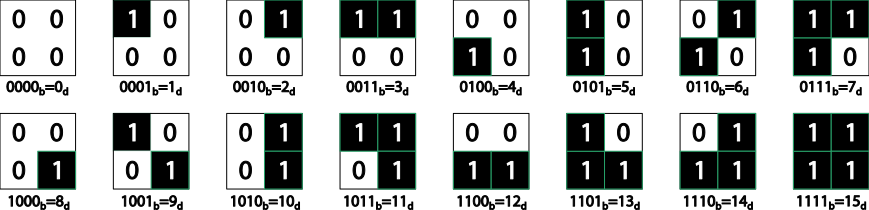
Amb aquesta correspondència, una solució toroidal amb les peces iguals en posició diferent seria
| 10 | 13 | 12 | 4 |
| 14 | 15 | 7 | 9 |
| 3 | 11 | 5 | 2 |
| 8 | 6 | 1 | 0 |
Segons els nostres càlculs aquesta és la única solució toroidal amb peces iguals en orientacions diferents llevat de simetries i posició inicial.
