Gira la roda per tal que totes les boletes quedin al dipòsit, llavors torna-la a girar per tal que es distribueixin entre les columnes. Abans de fer-ho: Pots preveure com quedarà?
Efectivament, no totes les barres s’omplen igual, aquesta silueta on les barres centrals són més altes que les laterals que recorda la forma de campana i s’anomena campana de Gauss.
Aquesta forma de campana amb els valors centrals més repetits i una disminució progressiva a banda i banda, apareix sovint mesurant objectes o fenòmens naturals. A vegades el mateix desgast indica la freqüència d’ús i crea de forma natural la forma acampanada.
- Ubicació: Sala Lluís Santaló
- Edat mínima: a partir de 6 anys.
- Temps requerit: 5 minuts.
- Nombre de participants: Una o més persones
- Paraules clau: Galton, Gauss distribució normal,
- Taxonomia: Probabilitat i estadística

Per què s'omplen les columnes d'aquesta manera?
Si l’aparell sols tingués menys bifurcació i sols 3 barres per recollir les boletes, com s’ompliria?
Pensa-ho abans de passar el ratolí per sobre la imatge per descobrir-ho
Efectivament, a la primera bifurcació les boletes es reparteixen per igual: la meitat per un costat i meitat per l’altre (en proporció 1-1).
A la següent bifurcació es tornen a dividir, una quarta part de les boletes per cada camí, però com que els dos camins centrals s’ajunten la proporció és 1-2-1
El mateix passa per les bifurcacions següents, les successives proporcions estan indicades amb vermell a la imatge, formen el conegut com a Triangle de Tartaglia.
Aquest conegut triangle amb múltiples propietats és forma sumant els dos números de la fila superior.
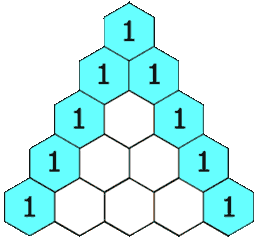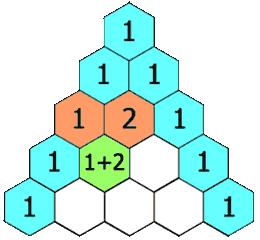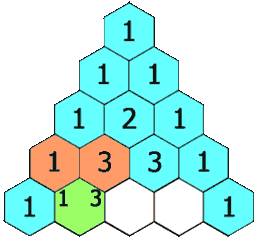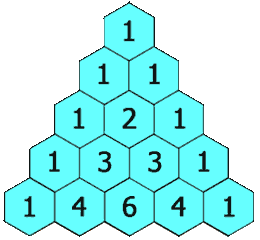
En aquest aparell concret amb 8 nivells de bifurcacions, les altures de les barres de boletes s’aproximen a les probabilitats teòriques:
1/ 256, 8/256, 28/256, 56/256, 70/256, 56/256, 28/256, 8/256, 1/ 256
Es tracta de la distribució binomial amb n=8 i p=0.5 dibuixada en blau.
En anar augmentant les bifurcacions aquesta distribució discreta s’aproxima a la distribució contínua anomenada normal o gaussiana dibuixada en verd a la imatge

Carl Friedrich Gauss
Johann Carl Friedrich Gauss (1777-1855), fou un dels matemàtics més influents de la història, és anomenat “Príncep dels matemàtics”. En qualsevol especialitat de la matemàtica actual es pot trobar algun concepte o resultat important que porta el seu nom.
La seva gran obra Disquisitiones arithmeticae, ha estat traduïda i publicada al català per l’IEC.
També podeu trobar una interessant biografia novel·lada seva titulada “L’home de la campana” escrita per Joan Girbau el 2015.

Imatge de la Viquipedia
Francis Galton
Francis Galton (1822-1911), inventor d’aquest aparell, era cosí de Charles Darwin, va ser un influent i polifacètic científic que va treballar sobre meteorologia, antropologia, herència, estadística, antropometria, biologia del desenvolupament i també psicologia.
És un exemple de la influència de la ideologia sobre les teories científiques. Va elaborar el terme eugenèsia que defensa l’existència de persones i grups superiors i inferiors i estudia formes de “millorar” la qualitat genètica humana. Aquesta teoria va ser la base sobre la qual es va fonamentar les polítiques de neteja ètnica i social que es van aplicar no sols a l’Alemanya nazi també als Estats Units, Canadà, Suècia, Suïssa o Austràlia.
Galton va invertir tot els seus diners i capacitats en mesurar i quantificar les característiques humanes per justificar la seva teoria, desenvolupant per això eines estadístiques avui valuoses.
Amb ulls actuals, és certament una part incòmoda de la història de l’estadística.

Imatge de la Viquipedia



