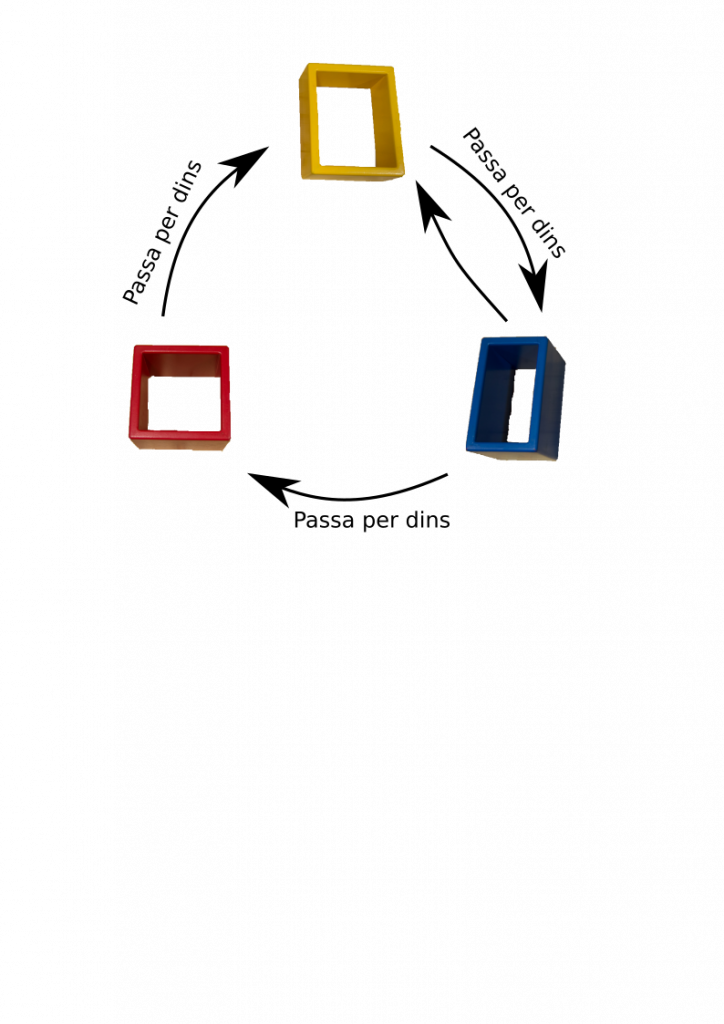Per ordenar aquestes 3 caixes, podem utilitzar molts criteris, per exemple: alçada, volum, mida del forat, tonalitat de color, etc.
Però et proposem investigar el criteri “POT PASSAR PER DINS”
Agafa les caixes blava i vermella, intenta passar la vermella pel forat de la blava, ara intenta passar la blava pel forat de la vermella. Quina caixa de les dues podem considerar “petita”.
Ara confronta la blava amb la groga. Quina és la “petita” segons aquest criteri.
I per acabar compara la groga i la vermella. Quina passa per dins?
En conseqüència, aquesta relació no estableix una ordenació de ls 3 caixes.
- Ubicació: Actualment, fora de l'exposició
- Edat mínima: a partir de 6 anys.
- Temps requerit: 5 minuts.
- Nombre de participants: Una o més persones
- Paraules clau:
- Taxonomia:

Les relacions no transitives
Aquesta relació que hem establert entre cada dues caixes és circular. No és una relació d’ordre.
Un altre exemple d’aquestes relacions és el joc “Pedra, paper, tisores”. El paper guanya la pedra, les tisores guanyen el paper, però les tisores perden enfront de la pedra. No hi ha guanyador absolut.
Per tal que una relació entre elements sigui d’ordenació cal que sigui transitiva. Una relació és transitiva si sempre que l’element A és més petit que l’element B i B és més petit que C , llavors A és més petit que C. La relació “POT PASSAR PER DINS” entre aquestes caixes NO és transitiva.
El mòdul “daus intransitius” de la sala d’estadística Lluís Santaló és un altre exemple d’aquest tipus de relació.