Col·loca els quadrats de manera que emplenin el marc.
Amb 11 quadrats formar un quadrat
L’any 1907, Sam Loyd va proposar aquest trencaclosques:
La Sra. Perkins va rebre un cobrellit fet amb 169 quadrats de seda. Com es pot dividir en el menor nombre possible de peces quadrades?
Aquí, les peces ja estan fetes, són 11 quadrats de costats 1,1,2,2,2,3,3,4,6,6 i 7 amb els que es pot reconstruir un quadrat de costat 13. Intenta fer-ho.
Amb 9 quadrats formar un rectangle
Aquesta és una versió en què l’objectiu és reconstruir un rectangle de costats 32 i 33 amb nou peces quadrades de costats 18,15,14,10,9,8,7,4 i 1
Intenta recompondre el quadrat.
Teniu la solució a la portada del Scientific American que hi ha una mica més avall.
Una altra descomposició:

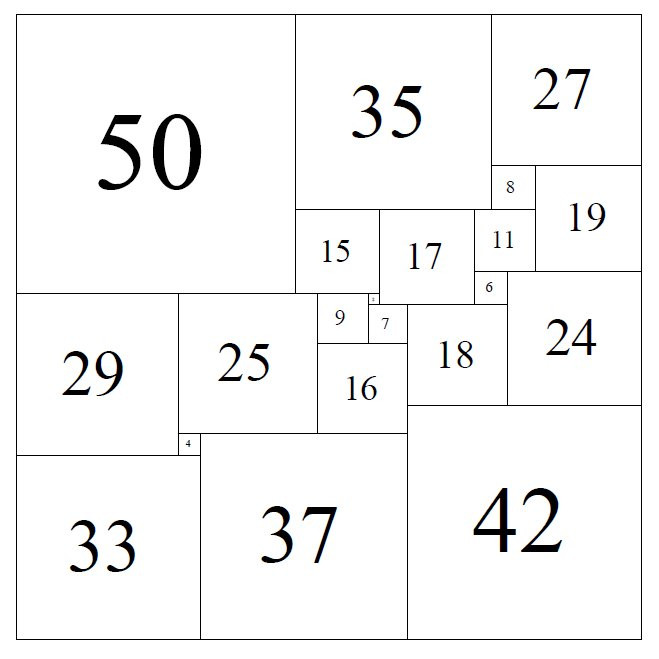
Aquesta és la descomposició del rectangle de 69×61 amb 9 quadrats de costats 2, 5, 7, 9, 16, 25, 28, 33 i 36
- Ubicació: sala Martin Gardner
- Edat mínima: a partir de 10 anys.
- Temps requerit: 5-10 minuts.
- Nombre de participants: Una o més persones
- Paraules clau: Combinatòria, quadrat, rectangle
- Taxonomia: Combinatòria, aritmètica
Solucions
Amb 11 peces un quadrat de costat 13

Amb 9 peces un rectangle 32x33
Aquesta dissecció va ser publicada l’any 1925 per Zbigniew Moroń.
L’any 1958 Martin Gardner en la seva columna al Scientific American en va fer esment.

La mínima dissecció PERFECTE del quadrat
El quadrat format per 11 quadrats d’aquest mòdul té peces repetides. És una bona solució del problema de descompondre el quadrat en quadrats, però no és la mínima, ja que hi ha una forma molt evident de dividir un quadrat en 4 quadrats iguals. Si penses un moment segur que la trobaràs.
Així que des del 1930, va iniciar-se la recerca de la descomposició d’un quadrat en quadrats diferents amb el mínim nombre de peces, el conegut com a dissecció PERFECTE del quadrat.
Després de successives descobertes de disseccions perfectes amb 55, 38, 26 i 25 quadrats, L’any 1978 AJW Duijvestij va trobar la descomposició en 21 quadrats que mostra la imatge de la dreta. L’any següent Paul Leeuw va demostrar que no n’hi havia altre amb menys peces.