Els sorprenents enrajolats no periòdics
En aquesta taula es proposa construir un sorprenent enrajolat. Cal col·locar les peces de forma que les corbes i els colors connectin bé. Llavors es comprova que es crea un enrajolat no periòdic. Comprovareu que malgrat s’arribi a un punt on no es pot seguir si es torna enrere traient peces ja col·locades, sempre podem engrandir el mosaic.
Que l’enrajolat sigui no periòdic vol dir, en altres paraules, que una còpia desplaçada no coincidirà mai amb l’original. A més, és autosimilar , els mateixos patrons pentagonals apareixen a escala més gran.
- Ubicació: Sala Martin Gardner
- Edat mínima: a partir de 6 anys.
- Temps requerit: 5-10 minuts.
- Nombre de participants: Una persona o més
- Paraules clau: mosaic, enrajolat periòdic, raó àuria
- Taxonomia: Geometria





Intuïtivament, quan ens imaginem un enrajolat ens ve al cap una estructura periòdica. És per això que quan el 1975 Martin Gardner va donar a conèixer aquests mosaics descoberts pel matemàtic, i físic anglès Roger Penrose, l’admiració i sorpresa van ser generals.
Les dues tessel·les varen ser anomenades per Penrose com a “kites” (estels) i “darts” (fletxes). L’estel és un quadrilàter convex d’angles 72º, 72º,72º i 144º i la fletxa un quadrilàter còncau d’angles interiors 36º, 72º, 36º, 216º. Es poden construir a partir de l’anomenat pentagrama pitagòric, símbol de la seva secta.

A l’inici de la construcció del mosaic, es crea un nucli central amb 5 tessel·les amb simetria pentagonal utilitzant l’angle de 72º o 360º/5. Sols hi ha dos models que permetin seguir. S’anomen “Sol” i “Estrella“. Proveu-los.

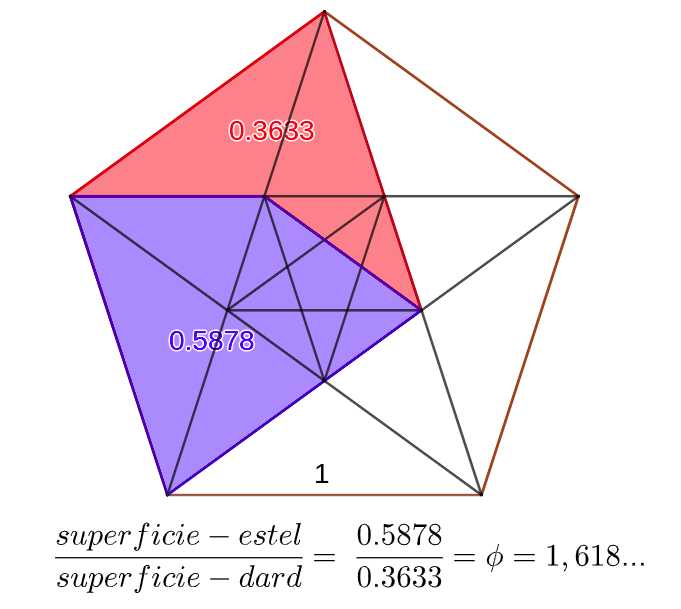
Les àrees de les dues peces estan en relació àuria
\frac{superficie-estel}{superficie-dard}= \frac{0,5878}{0.3633}=\phi =1,618… i
Penrose va descobrir una forma de modificar un d’aquests enrajolats per fer-ne un altre amb peces més grans. El va anomenar inflació.
La inflació consisteix, tal com mostra el dibuix, en partir per la meitat les fletxes i unir-les de la forma indicada, d’aquesta manera s’obté la fletxa i el dard marcats amb verd, que són el doble de les originals. Aquest procés pot repetir-se indefinidament i també fer-se en sentit contrari aconseguint peces la meitat de les originals, llavors s’anomena deflació.
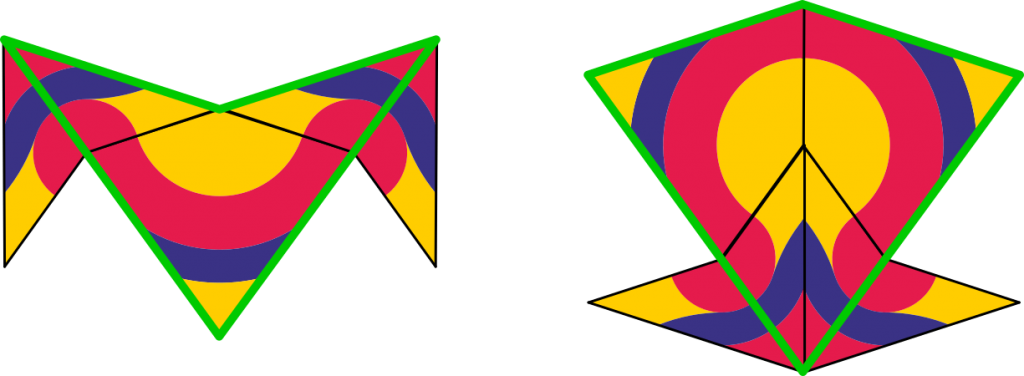
Enllaços i material descarregable
Altres mòduls
En aquest mòdul les circumferències de diferent mida poden rodar sobre una altra fixada, els engranatges permeten fer-ho sense que rellisquin. Els corbes que s’obtenen són les hipocicloides (si es fan rodar per l’interior) i les hipocicloides (si es fan rodar per l’exterior). En funció de les mides relatives de la circumferència fixa i la que roda s’obtenen els diferents tipus d’aquestes corbes.
Les 5 peces de fusta de diferents tonalitats amb què està construït aquest con mostren els 4 tipus de seccions: Circumferència, el·lipse, paràbola i hipèrbola.
La primera part consisteix en un engranatge de 50 dents a l’interior del qual pot girar un cercle de 25 dents, els 5 punts de color del cercle segueixen els 5 diàmetres. La segona part és una peça pentagonal amb els 5 vèrtexs de color situats a la mateixa posició que abans. El pentàgon pot girar suaument gràcies als encaixos inserits a les rases construïdes com els diàmetres de la primera part.



