The surprising non-periodic tiles
In this table it is proposed to build a surprising tiling. It is necessary to place the pieces so that the curves and colors connect well. Then it is checked that a non-periodic tiling is created. You will see that despite reaching a point where you can not follow if you go backwards removing pieces already placed, we can always enlarge the mosaic.
That the tiling is non-periodic means, in other words, that a displaced copy will never match the original. In addition, it is self-assimilating, the same pentagonal patterns appear on a larger scale.
- Hotel Area: Sala Martin Gardner
- Minimum age: from 6 years old.
- Required time: 5-10 minutes.
- Number of participants: One person or more
- Keywords: mosaic, periodic tiling, golden ratio
- Taxonomy: Geometry





Intuitively, when we imagine a tiling, a periodic structure comes to mind. That is why when in 1975 Martin Gardner unveiled these mosaics discovered by the Mathematician, and English physicist Roger Penrose, the admiration and surprise were general.
The two tesses were named by Penrose as "kites" (stars) and "darts" (arrows). The star is a convex quadrilateral of angles 72º, 72º, 72º and 144º and the arrow a concave quadrilateral of inner angles 36º, 72º, 36º, 216º. They can be built from the so-called Pythagorean staff, symbol of their sect.

At the beginning of the construction of the mosaic, a central core is created with 5 tesses with pentagonal symmetry using the angle of 72º or 360º/5. There are only two models that allow you to follow. They are called "Sun" and "Star". Try them.

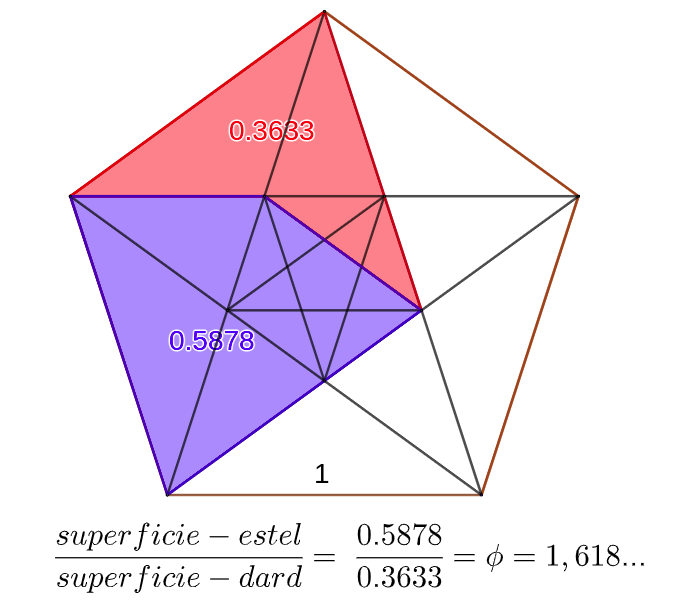
The areas of the two pieces are in golden ratio
\frac{superficie-estel}{superficie-dard}= \frac{0,5878}{0.3633}=\phi =1,618… i
Penrose discovered a way to modify one of these tiling to make another with larger pieces. He called it inflation.
Inflation consists, as the drawing shows, by spliting the arrows in half and joining them in the indicated shape, in this way you get the arrow and the dart marked with green, which are twice the original ones. This process can be repeated indefinitely and also done in the opposite direction achieving pieces half of the originals, then it is called deflation.
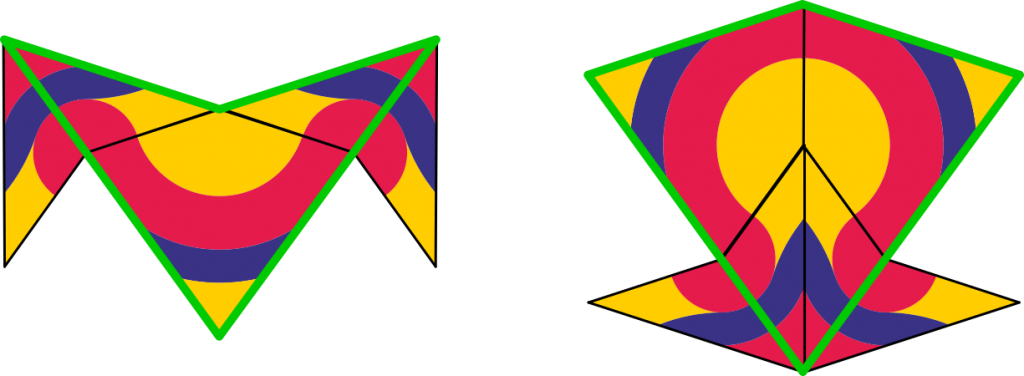
Links and downloadable material
Other Modules
In this module the circumferences of different sizes can roll on another fixed, the gears allow to do it without slipping. The curves obtained are hypocycloids (if rolled inside) and hypocycloids (if rolled on the outside). Depending on the relative sizes of the fixed circumference and the one that rolls, the different types of these curves are obtained.
The 5 pieces of wood of different shades with which this cone is built show the 4 types of sections: Circumference, ellipse, parabola and hyperbola.
The first part consists of a gear of 50 teeth inside which can rotate a circle of 25 teeth, the 5 color points of the circle follow the 5 diameters. The second part is a pentagonal piece with the 5 color vertices located in the same position as before. The pentagon can rotate gently thanks to the laces inserted in the trenches built as the diameters of the first part.



