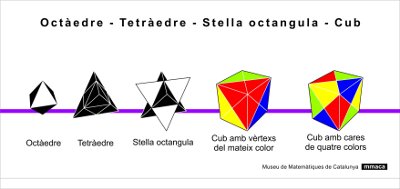
Segueix aquesta seqüència de construcció:
Parteix de l’octaedre, és la peça blanca i negra de 8 cares triangulars.
Enganxa-hi fent servir els imants els 4 tetraedres negres. El resultat un tetraedre negre d’aresta doble.
Enganxa-hi els 4 tetraedres blancs. El resultat és una estrella de 8 puntes (Stella octangula), formada per dos tetraedres intersecats.
Per acabar posa les peces vermelles, grogues, verdes i blaves per obtenir un cub.
Ho pots fer de forma que les peces d’un mateix color coincideixin en un vèrtex?
Ho pots fer de forma que a cada cara del cub hi hagi els 4 colors?
- Ubicació: Sala Pere Puig Adam
- Edat mínima: a partir de 6 anys.
- Temps requerit: 5 minuts.
- Nombre de participants: Una o més persones
- Paraules clau: poliedres, tetraedre, octaedre, cub, stella octangula.
- Taxonomia: Geometria





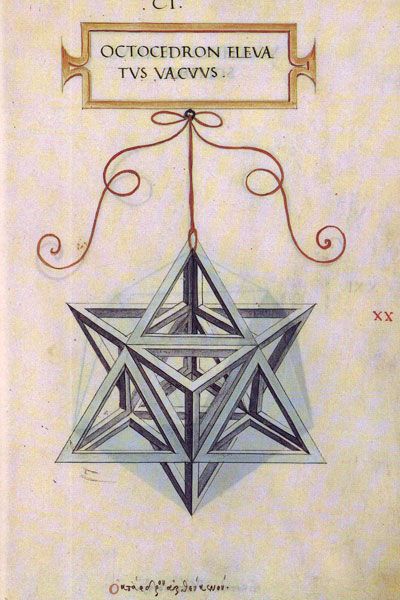
L'estrella de 8 puntes o Stella octangula
Aquesta figura va ser dibuixada per Leonardo de Vinci com a il·lustració de l’obra la Divina Proportione (1509) de Luca Pacioli, amb el nom de Octocedron Elevatus Vacuus.
Més endavant, Johannes Kepler en el seu llibre De Nive Sexangula (1611). li va donar el nom d’Stella Octangula
Com heu pogut comprovar malgrat el seu aspecte punxegut, els seus vèrtexs estan situats exactament als vèrtexs d’un cub.
Els volums dels tetraedres, l'octaedre i el cub
- Totes les peces tetraèdriques d’aquest mòdul tenen el mateix volum. Per justificar-ho, comprova que posant les peces de color adequadament, totes tenen la mateixa base (un triangle equilàter) i la mateixa altura (posa de costat un tetraedre de color i un negre). Anomenem aquest volum T.
- Comparem el volum del tetraedre negre d’aresta doble que s’ha construït al principi amb el volum T d’un dels tetraedres regulars petits. Són figures semblants de raó 2. La raó dels volums és 2³. Així doncs, el tetraedre negre d’aresta doble té volum 8T.
- Es pot calcular el volum de l’octaedre de l’interior del tetraedre negre d’aresta restant de 8T els tetraedres que hi hem enganxat. Quin és doncs el volum de l’octaedre?
- I també podem calcular el volum del cub final en funció de T comptant quants tetraedres s’han posat sobre l’octaedre. Recompta’ls per comprovar que el cub final té volum 24T
Un altre possible enfoc sobre els càlculs dels volums
Mòduls relacionats
- Al mòdul Encaixant poliedres d’aquesta mateixa sala es pot veure un cub amb un tetraedre encaixat dins seu de la mateixa forma que ho estan en aquest mòdul.
- El mòdul Longitud, superfície i volum d’aquesta sala mostra com calen 8 esferes petites per equilibrar una esfera del doble de diàmetre. És el mateix motiu pel qual el tetraedre d’aresta doble que s’ha muntat en aquest mòdul té volum 8 vegades el del tetraedre petit semblant.
