En aquest aparell, hi ha dues pistes una recta i una altra en forma d’U molt oberta. Les dues pistes coincideixen en dos punts, el punt inicial a l’extrem superior i el punt final mitja altura de l’altre costat. Si des del punt més alt deixem anar a la vegada dues pilotes una per cada pista:
Quina arribarà abans al punt final? Arribaran al mateix temps?





- Ubicació en el museu: Sala Pere Puig Adam
- Edat mínima: a partir de 4 anys.
- Temps requerit: 5-10 minuts.
- Nombre de participants: 1 o més.
Funcionament
Si ho heu provat, haureu observat que, clarament, la pilota que fa el recorregut corbat arriba molt abans que la que ha fet el recorregut recte.
Això pot ser un pèl sorprenent, ja que tenim après que “la distància més curta entre dos punts és la línia recta”. Cal recordar que la pregunta inicial es referia al temps no pas a la distància, la pilota que es troba amb un pendent més fort a l’inici agafa més velocitat.
Hi ha, però, moltes formes possibles de fer aquesta corba: arc de circumferència, paràbola, el·lipse, etc. Justament, la d’aquest aparell, és la forma que aconsegueix la trajectòria més ràpida. S’anomena cicloide, és la trajectòria d’un punt d’una circumferència en rodar sobre una recta. En el mòdul, la cicloide està en posició invertida amb les puntes cap avall.
Context històric
Al segle XVII, es va plantejar el problema de la corba tautòcrona (dels prefixos grecs tauto- que vol dir mateix i chrono temps ), es tractava de trobar la corba on un objecte triga el mateix a arribar al punt més baix independent del punt de partida. Christiaan Huygens el 1659 va aconseguir demostrar que la corba amb aquesta propietat és la cicloide.
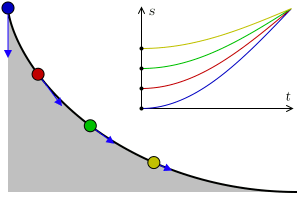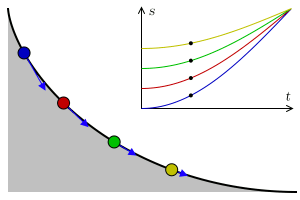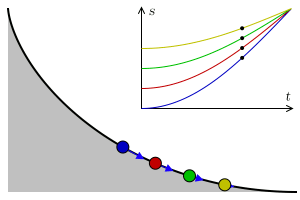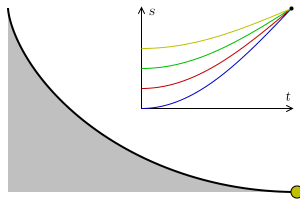
Podeu comprovar aquesta propietat a l’aparell del museu. Deixeu anar a la vegada dues pilotes una a cada costat de la cicloide però a diferents alçades, veureu que arriben al punt més baix simultàniament.
Johann Bernoulli el 1696 va proposar a la comunitat matemàtica el problema de trobar la braquistòcrona, (dels prefixos grecs brachistos– que vol dir el més curt, i chrono temps ) és a dir la corba de descens més ràpid. Johann Bernoulli ja sabia que la solució és, un altre cop, la cicloide. Les respostes i els treballs de Leibniz, Newton, Jakob Bernoulli, Leibniz i Guillaume de Hôpital i Jakob Bernoulli sobre aquest problema varen portar al desenvolupament de noves i importants eines matemàtiques. És per això que la cicloide ha rebut el nom d’Helena de la Geometria.
Material d'ampliació descarregable
La Gemma Ramírez ha fet el seu Treball Final de Grau de Matemàtiques de la Universitat de Barcelona com a projecte d’Aprenentatge i Servei amb el MMACA sobre aquesta corba.
A l’article hi trobareu un estudi de les propietats geomètriques i físiques de la cicloide, un repàs històric de les aportacions dels diferents matemàtics així com un estudi amb les eines actuals.
Mòduls relacionats
En aquest mòdul les circumferències de diferent mida poden rodar sobre una altra fixada, els engranatges permeten fer-ho sense que rellisquin. Els corbes que s’obtenen són les hipocicloides (si es fan rodar per l’interior) i les hipocicloides (si es fan rodar per l’exterior). En funció de les mides relatives de la circumferència fixa i la que roda s’obtenen els diferents tipus d’aquestes corbes.
Les 5 peces de fusta de diferents tonalitats amb què està construït aquest con mostren els 4 tipus de seccions: Circumferència, el·lipse, paràbola i hipèrbola.
La primera part consisteix en un engranatge de 50 dents a l’interior del qual pot girar un cercle de 25 dents, els 5 punts de color del cercle segueixen els 5 diàmetres. La segona part és una peça pentagonal amb els 5 vèrtexs de color situats a la mateixa posició que abans. El pentàgon pot girar suaument gràcies als encaixos inserits a les rases construïdes com els diàmetres de la primera part.



