With these 7 pieces, build a cube of 3 x 3 x 3, that is, 27 units.

- Hotel Area: Sala Martin Gardner
- Minimum age: from 6 years old.
- Required time: 5 minutes.
- Number of participants: One or more people
- Paraules clau: poliminos, cub, puzle
- Taxonomia: Matemàtica recreativa
The origin of this puzzle
This space puzzle was devised in 1926 by the Danish scientist and poet Piet Hein. It is known and used everywhere, even part of
psychological tests. Here you can download (PDF) some original instructions from the year 1969 of this puzzle.

Many more figures to make
In addition to the cube, it is possible to build many other figures, here is a collection of them

The solutions
One, two, three, ... 240 solutions!
Despite looking amazing, there are no less than 240 different ways to form the 3x3x3 cube without counting symmetries and turns. So this puzzle doesn't end up being built once. To exhaust it you will have to find them all!
The names of the pieces
These are the names by which pieces are usually called
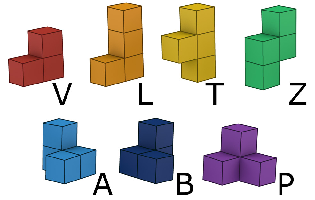
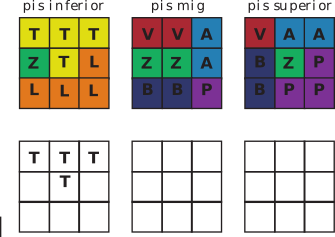
The position of the T
A peculiarity of all the solutions is that the long bar of the T piece is always located on one of the edges of the cube, never on the central floor.
A demonstration is as follows: once resolved, there will be 8 cubes located at the vertices, each of the 5 pieces V, Z, A, B, P can occupy at most one of these positions at the vertices, the piece L can occupy two of these positions. So, without part T, there are at most 7 vertices occupied, so the T must occupy the remaining vertex.
The registration of solutions
The fact that, in all 240 solutions, the T is located on an edge, makes it easier for us to register and compare solutions. Once resolved, we can always turn the cube so that the T is on the lower floor and located behind.
Here is a solution noted, there are only 239 left to find. Then the grid is prepared for the next solution with the T already placed.
Polycubes
Of these figures formed by the union of cubes we can call them polycubes. Besides the 7 in the Soma Cube, are there more? We can study it systematically.
Tetracubes
Of 4-unit polycubes or tetracubes there are 8 (finding them is a good exercise), six are non-convex, they are precisely the pieces of the Soma.
The other two tetracubes (think what they are like!) are convex.
So the 7 pieces of the Soma are precisely: all non-convex polycubes of 3 and 4 units.
The Bicube
The Two Tricubes

These are the only two tricubes, they have a characteristic that differentiates them: convexity. A figure is called a convex if the entire segment that joins any pair of points is inside the figure. Thus the polycube on the left is convex. The second tricube, piece V, however, is not, since the segment that joins the points M and N has an outer part. It is a non-convex or concave figure.
Material descarregable i en línia
Els cubs de plàstic encaixables són uns dels materials imprescindibles a l’aules de matemàtiques de tots els nivells escolars. Trobareu moltísimes propostes, per exemple: aquesta de l’ARC o aquest vídeo del CREAMAT

